
KOPUŁA - MODEL POWŁOKA
Kopuła, identyczna jak w przykładzie poprzednim, zostanie teraz rozwiązana
z wykorzystaniem elementu trójkątnego trzywęzłowego powłokowego. Korzystanie z takiego
elementu jest konieczne w przypadku powłok obrotowo-symetrycznych przy niesymetrycznym
obciążeniu.
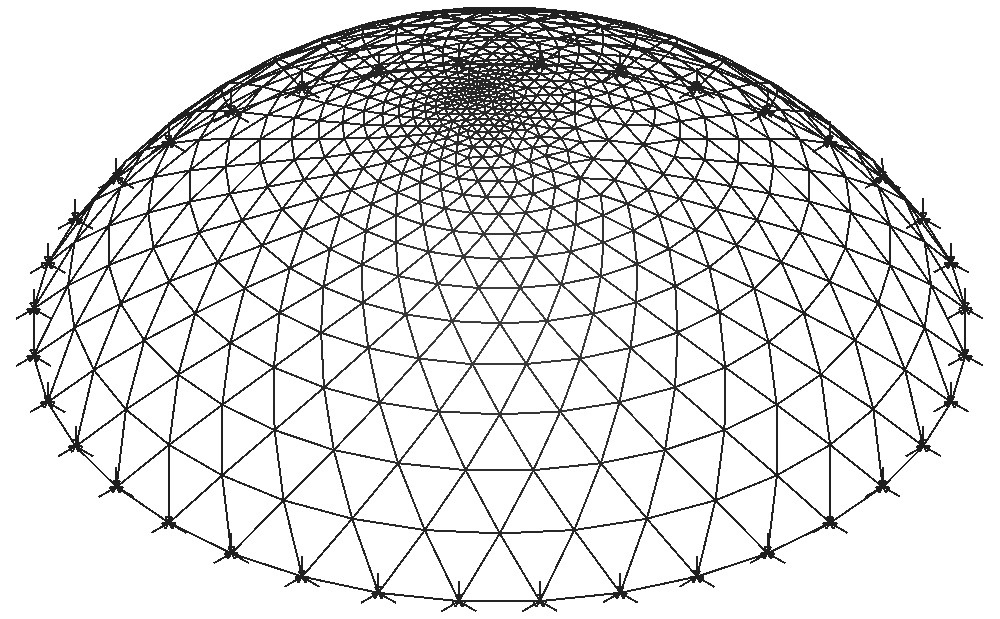
Rys.1. Przyjęty model.
Siatkę węzłów i elementów utworzono korzystając z generatora pt.
System FEAS zawiera zestaw generatorów do generacji siatek na typowych
figurach i powłokach ( h prym).
Kopuła w zadaniu jest zamknięta od góry, a używany
przez nas generator zagęszcza siatkę podziału ku wierzchołkowi kopuły, dlatego
siatkę zbudowano z dwóch części. Pierwsza część wygenerowana generatorem pt,
drugą z wykorzystaniem generatora tgr (domknięcie kopuły).
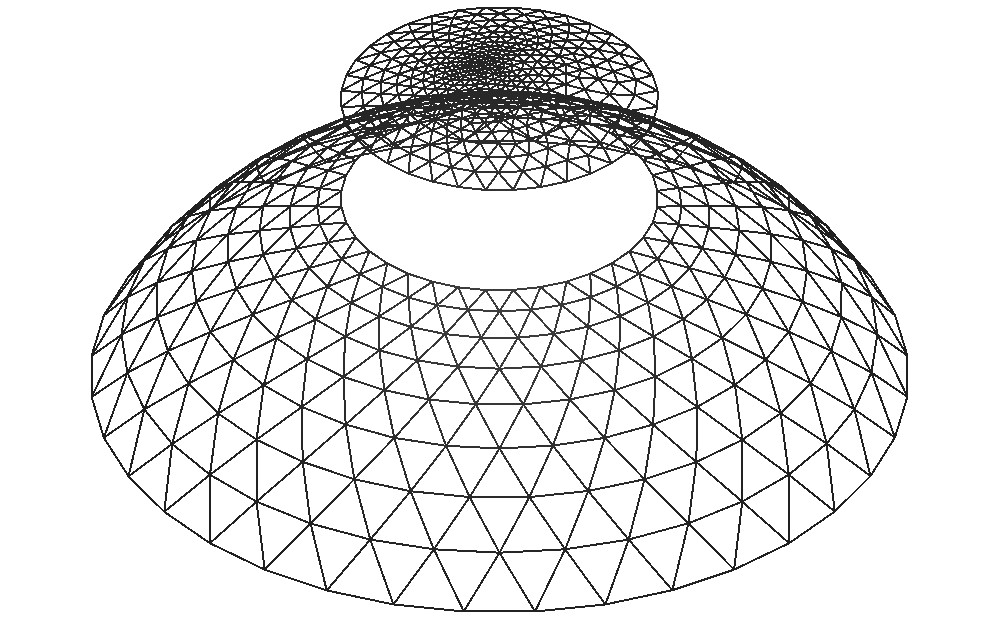
Rys.2. Wygenerowane siatki.
Ze względu na to, że komenda tgr tworzy siatkę na płaszczyźnie, uwypuklenia jej
dokonano poza systemem FEAS (dopisano odpowiednie wartości współrzędnej z).
Do tego celu można wykorzystać arkusz kalkulacyjny, albo edytor tekstu.
Następnie korzystając z komendy cu (czytanie uzupełniające) wczytano dane do
zadania z pliku (nazwa pliku DANE).
Przygotowanie siatki węzłów i elementów polegało na:
- wygenerowaniu komendą pt-sf dolnej części siatki,
- wygenerowaniu siatki rozpiętej między węzłami
górnego skrajnego południka dolnej części powłoki. W tym etapie
wykorzystano metodę triangularyzacji -- komenda tgr,
- uwypukleniu wcześniej stworzonej siatki. Ponieważ triangularyzacja
przebiega na płaszczyźnie konieczne jest nadanie węzłom odpowiednich
wartości współrzędnej z. Do tego celu wykorzystano arkusz kalkulacyjny.
- przygotowaniu pliku z danymi. Opis formatu danych znajduje się w
podręczniku podsystemu OK, lub w helpie komendy cu,
- wczytaniu danych z pliku komendą cu
- zszyciu obu siatek komenda zw.
ROZPOCZĘCIE PRACY.
$ feas - wejście do systemu feas,
FEAS> - system zgłasza gotowość do pracy,
OPIS KONSTRUKCJI.
FEAS> ok
- wejście do podsystemu OK - Opis Konstrukcji,
Podaj rodzaj konstrukcji po-i - powłoka izotropowa,
generowanie dolnej części siatki
OK> pt-sf - wykorzystano prymityw trójkątny sferyczny,
NazWez ?> w-1 - wzorcowa nazwa generowanych wezłów,
NazEl ?> e-1 - wzorcowa nazwa generowanych elementów,
pn ?> 20 - kąt między biegunem a górnym skrajnym południkiem,
pd ?> 61.929 - kąt między biegunem a dolnym skrajnym południkiem,
R ?> 11.333 - promień krzywizny powłoki,
n ?> 36 - gęstość podziału wzdłuż równoleżników,
liczba wygenerowanych: węzłów = 324, elementów = 576
- nowo powstałe węzły mają nazwy od w-1 do w-324, elementy od e-1 do e-576.
czytanie węzłów i elementów siatki zamykającej powłokę
OK> cu dane - czytanie uzupełniające danych z pliku "DANE",
NPozW >ww-1 - wzorcowa nazwa wczytywanych węzłów,
NPozE >ee-1 - wzorcowa nazwa wczytywanych elementów,
- nowo wczytane węzły mają nazwy od ww-1 do ww-356, elementy od ee-1 do ee-674,
zszywanie siatek
OK> zw ww-1 do ww-36 w-289 do w-324 0.001
Wezel: W-289 zastepowany jest wezlem: WW-1 [T/N/W/K] t
Odpowiednie węzły z siatki dolnej o nazwach "w-" zostały zastąpione przez
węzły siatki "zamykającej" o nazwach "ww-". Tolerancja 0.001 określa
dopuszczalną odległość między sąsiadującymi ze sobą węzłami, które
mają być zastąpione jednym. Węzły od w-289 do w-324 przestają istnieć.
definiowanie geometrii i materiału
OK> g geo - def. geometrii, której nadano nazwę geo,
Geom:H=0 ? > 0.06 - powłoka ma grubość 0.06m,
OK> m - def. materiału o nazwie mat,
MAT:Ro=0 ? >5096.84 - gęstość masy [kg/m3],
MAT:E=0 ? >0.3e11 - współczynnik sprężystości [N/m2],
MAT:Ni=0 ? >0.16667 - współczynnik Poissona,
MAT:AlfT=0 ? > - współczynnik rozszerzalności termicznej (nie jest uwzględniany),
przypisanie elementom materiału i geometrii
OK> pe e-1 do e-576 ee-1 do ee-674 mat geo
warunki brzegowe
OK> wb w-1 do w-36 ux uy uz - odebranie możliwości przesuwu węzłom podporowym,
sprawdzenie poprawności opisu i zapisanie zadania
OK> spr
OK> zap powloka
OK> .. - wyjście z podsystemu OK,
ROZWIĄZANIE ZADANIA
FEAS>ro scw1 - SCW1.ALG - algorytm do
rozwiązania konstrukcji obciążonej ciężarem własnym (plik taki sam jak w zadaniu
poprzednim ale uwzględniający działanie sił grawitacji w kierunku osi z),
WYNIKI OBLICZEN
Z uwagi na dużą liczbę elementów, a co za tym idzie dużą liczbę wyników,
ograniczono się do przedstawienia rozwiązania zadania tylko w niektórych
elementach. Aby móc porównać wyniki z rozwiązaniem powłoki obrotowo
symetrycznej wybrano elementy leżące w różnej odległości od osi, w
przybliżeniu na wspólnym południku. Przyjęto założenie, że siły
wewnętrzne w elementach równo oddalonych od osi symetrii są takie same.
Wybrane elementy przedstawiono na rysunku poniżej. Są to: e-70 do e-574 co
72, e-71 do e-575 co 72, ee-70, 69, 135, 139, 642, 641, 633, 624, 610, 600,
563, 550.
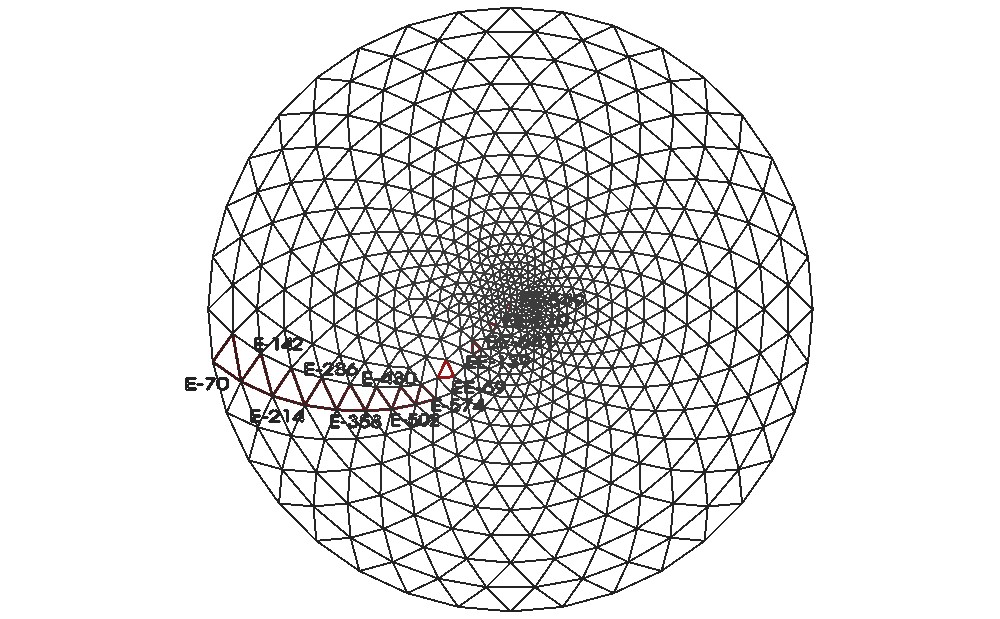
Rys.3. Położenie wybranych elementów.
FEAS>ws - wywołanie podsystemu WS,
WS> dp - otwarcie pliku w którym zostaną zapisane wyniki,
WS> ne e-70 do e-574 co 72 /p - opcja /p oznacza drukowanie do pliku,
WS> ne e-71 do e-575 co 72 /p
WS> ne ee-70 ee-69 ee-135 ee-139 ee-642 ee-641 ee-633 ee-624 ee-610 ee-600 /p
WS> ne ee-563 ee-550 /p
WS> .. - wyjście z podsystemu WS,
FEAS>.. - zakończenie pracy,
Wyniki, przemieszczenia oraz siły wewnętrzne, otrzymane dla danej powłoki
prz użyciu elementu powłokowego oraz elementu powłoki osiowo-symetrycznej
są porównywalne. Zestawienie przemieszczeń węzłowych w wybranych
punktach oraz sił wewnętrznych w wybranych elementach, poniżej.
siły wewnętrzne
lp numer N1=Nt N2=Ns lp numer N1=Nt N2=Ns
1 ee-550 -16989 -17109 15 e-502 -13415 -17444,7
2 ee-563 -16987,4 -17111,7 16 e-503 -12282,3 -17928,7
3 ee-600 -16988,1 -17080,4 17 e-430 -12225,6 -17587,4
4 ee-610 -16968,5 -16993,8 18 e-431 -10833,8 -18471,7
5 ee-624 -16771,2 -16978,6 19 e-358 -10728,9 -17842,1
6 ee-633 -16519,2 -17035,4 20 e-359 -8555,38 -19127,3
7 ee-641 -16496,2 -16884,4 21 e-286 -8412,49 -18269,9
8 ee-642 -16180,6 -16980,1 22 e-287 -5758,82 -19795,2
9 ee-139 -15782,9 -17052,8 23 e-214 -5597,87 -18829,6
10 ee-135 -14933,9 -17262,5 24 e-215 -2406,1 -20715,1
11 ee-70 -14424,7 -17467,8 26 e-143 3523,686 -22098,1
13 e-574 -14445 -17483,1 27 e-703 536,225 -22022,9
14 e-575 -13522,5 -18007,9 28 e-71 -3701,98 -22211,4
przemieszczenia
lp nazwa ugięcie
węzła [m]
1 ww-40 -0,00021
2 ww-39 -0,00021
3 ww-38 -0,0002
4 ww-37 -0,00019
5 ww-36 -0,00018
6 w-288 -0,00016
7 w-252 -0,00015
8 w-216 -0,00013
9 w-180 -0,00011
10 w-144 -7,8E-05
11 w-108 -4,4E-05
12 w-72 1,67E-06
13 w-36 0
Kopuła, identyczna jak w przykładzie poprzednim, zostanie teraz rozwiązana z wykorzystaniem elementu trójkątnego trzywęzłowego powłokowego. Korzystanie z takiego elementu jest konieczne w przypadku powłok obrotowo-symetrycznych przy niesymetrycznym obciążeniu.

Rys.1. Przyjęty model.
Siatkę węzłów i elementów utworzono korzystając z generatora pt. System FEAS zawiera zestaw generatorów do generacji siatek na typowych figurach i powłokach ( h prym).
Kopuła w zadaniu jest zamknięta od góry, a używany przez nas generator zagęszcza siatkę podziału ku wierzchołkowi kopuły, dlatego siatkę zbudowano z dwóch części. Pierwsza część wygenerowana generatorem pt, drugą z wykorzystaniem generatora tgr (domknięcie kopuły).

Rys.2. Wygenerowane siatki.
Ze względu na to, że komenda tgr tworzy siatkę na płaszczyźnie, uwypuklenia jej dokonano poza systemem FEAS (dopisano odpowiednie wartości współrzędnej z). Do tego celu można wykorzystać arkusz kalkulacyjny, albo edytor tekstu. Następnie korzystając z komendy cu (czytanie uzupełniające) wczytano dane do zadania z pliku (nazwa pliku DANE).
Przygotowanie siatki węzłów i elementów polegało na:
- wygenerowaniu komendą pt-sf dolnej części siatki,
- wygenerowaniu siatki rozpiętej między węzłami górnego skrajnego południka dolnej części powłoki. W tym etapie wykorzystano metodę triangularyzacji -- komenda tgr,
- uwypukleniu wcześniej stworzonej siatki. Ponieważ triangularyzacja przebiega na płaszczyźnie konieczne jest nadanie węzłom odpowiednich wartości współrzędnej z. Do tego celu wykorzystano arkusz kalkulacyjny.
- przygotowaniu pliku z danymi. Opis formatu danych znajduje się w podręczniku podsystemu OK, lub w helpie komendy cu,
- wczytaniu danych z pliku komendą cu
- zszyciu obu siatek komenda zw.
| $ feas | - wejście do systemu feas, |
| FEAS> | - system zgłasza gotowość do pracy, |
| FEAS> ok | - wejście do podsystemu OK - Opis Konstrukcji, |
| Podaj rodzaj konstrukcji po-i | - powłoka izotropowa, |
| OK> pt-sf | - wykorzystano prymityw trójkątny sferyczny, |
| NazWez ?> w-1 | - wzorcowa nazwa generowanych wezłów, |
| NazEl ?> e-1 | - wzorcowa nazwa generowanych elementów, |
| pn ?> 20 | - kąt między biegunem a górnym skrajnym południkiem, |
| pd ?> 61.929 | - kąt między biegunem a dolnym skrajnym południkiem, |
| R ?> 11.333 | - promień krzywizny powłoki, |
| n ?> 36 | - gęstość podziału wzdłuż równoleżników, |
| liczba wygenerowanych: węzłów = 324, elementów = 576 | - nowo powstałe węzły mają nazwy od w-1 do w-324, elementy od e-1 do e-576. |
| OK> cu dane | - czytanie uzupełniające danych z pliku "DANE", |
| NPozW >ww-1 | - wzorcowa nazwa wczytywanych węzłów, |
| NPozE >ee-1 | - wzorcowa nazwa wczytywanych elementów, |
| - nowo wczytane węzły mają nazwy od ww-1 do ww-356, elementy od ee-1 do ee-674, |
| OK> zw ww-1 do ww-36 w-289 do w-324 0.001 |
| Wezel: W-289 zastepowany jest wezlem: WW-1 [T/N/W/K] t |
Odpowiednie węzły z siatki dolnej o nazwach "w-" zostały zastąpione przez
węzły siatki "zamykającej" o nazwach "ww-". Tolerancja 0.001 określa
dopuszczalną odległość między sąsiadującymi ze sobą węzłami, które
mają być zastąpione jednym. Węzły od w-289 do w-324 przestają istnieć.
Z uwagi na dużą liczbę elementów, a co za tym idzie dużą liczbę wyników,
ograniczono się do przedstawienia rozwiązania zadania tylko w niektórych
elementach. Aby móc porównać wyniki z rozwiązaniem powłoki obrotowo
symetrycznej wybrano elementy leżące w różnej odległości od osi, w
przybliżeniu na wspólnym południku. Przyjęto założenie, że siły
wewnętrzne w elementach równo oddalonych od osi symetrii są takie same.
Wybrane elementy przedstawiono na rysunku poniżej. Są to: e-70 do e-574 co
72, e-71 do e-575 co 72, ee-70, 69, 135, 139, 642, 641, 633, 624, 610, 600,
563, 550.
Rys.3. Położenie wybranych elementów.
Wyniki, przemieszczenia oraz siły wewnętrzne, otrzymane dla danej powłoki
prz użyciu elementu powłokowego oraz elementu powłoki osiowo-symetrycznej
są porównywalne. Zestawienie przemieszczeń węzłowych w wybranych
punktach oraz sił wewnętrznych w wybranych elementach, poniżej.
OK> g geo - def. geometrii, której nadano nazwę geo,
Geom:H=0 ? > 0.06 - powłoka ma grubość 0.06m,
OK> m - def. materiału o nazwie mat,
MAT:Ro=0 ? >5096.84 - gęstość masy [kg/m3],
MAT:E=0 ? >0.3e11 - współczynnik sprężystości [N/m2],
MAT:Ni=0 ? >0.16667 - współczynnik Poissona,
MAT:AlfT=0 ? > - współczynnik rozszerzalności termicznej (nie jest uwzględniany),
OK> pe e-1 do e-576 ee-1 do ee-674 mat geo
OK> wb w-1 do w-36 ux uy uz - odebranie możliwości przesuwu węzłom podporowym,
OK> spr
OK> zap powloka
OK> .. - wyjście z podsystemu OK,
FEAS>ro scw1 - SCW1.ALG - algorytm do
rozwiązania konstrukcji obciążonej ciężarem własnym (plik taki sam jak w zadaniu
poprzednim ale uwzględniający działanie sił grawitacji w kierunku osi z),

FEAS>ws - wywołanie podsystemu WS,
WS> dp - otwarcie pliku w którym zostaną zapisane wyniki,
WS> ne e-70 do e-574 co 72 /p - opcja /p oznacza drukowanie do pliku,
WS> ne e-71 do e-575 co 72 /p
WS> ne ee-70 ee-69 ee-135 ee-139 ee-642 ee-641 ee-633 ee-624 ee-610 ee-600 /p
WS> ne ee-563 ee-550 /p
WS> .. - wyjście z podsystemu WS,
FEAS>.. - zakończenie pracy,
siły wewnętrzne
lp numer N1=Nt N2=Ns lp numer N1=Nt N2=Ns
1 ee-550 -16989 -17109 15 e-502 -13415 -17444,7
2 ee-563 -16987,4 -17111,7 16 e-503 -12282,3 -17928,7
3 ee-600 -16988,1 -17080,4 17 e-430 -12225,6 -17587,4
4 ee-610 -16968,5 -16993,8 18 e-431 -10833,8 -18471,7
5 ee-624 -16771,2 -16978,6 19 e-358 -10728,9 -17842,1
6 ee-633 -16519,2 -17035,4 20 e-359 -8555,38 -19127,3
7 ee-641 -16496,2 -16884,4 21 e-286 -8412,49 -18269,9
8 ee-642 -16180,6 -16980,1 22 e-287 -5758,82 -19795,2
9 ee-139 -15782,9 -17052,8 23 e-214 -5597,87 -18829,6
10 ee-135 -14933,9 -17262,5 24 e-215 -2406,1 -20715,1
11 ee-70 -14424,7 -17467,8 26 e-143 3523,686 -22098,1
13 e-574 -14445 -17483,1 27 e-703 536,225 -22022,9
14 e-575 -13522,5 -18007,9 28 e-71 -3701,98 -22211,4
przemieszczenia
lp nazwa ugięcie
węzła [m]
1 ww-40 -0,00021
2 ww-39 -0,00021
3 ww-38 -0,0002
4 ww-37 -0,00019
5 ww-36 -0,00018
6 w-288 -0,00016
7 w-252 -0,00015
8 w-216 -0,00013
9 w-180 -0,00011
10 w-144 -7,8E-05
11 w-108 -4,4E-05
12 w-72 1,67E-06
13 w-36 0