
NAZIEMNY ZBIORNIK NA CIECZ
Dla danego zbiornika wypełnionego wodą znaleźć przemieszczenia oraz siły
wewnętrzne.
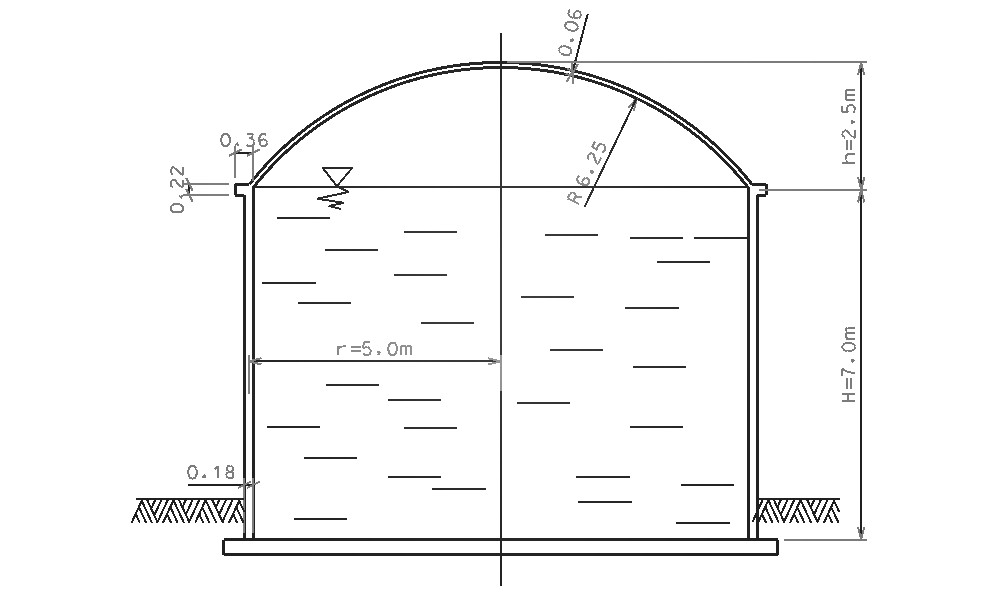
Rys.1. Zbiornik na wodę.
Dane: beton B-25, E=3107 2kPa, ni=1/6, gammac= 10 kN/m32 * 1.1 = 11kN/m32
(1.1 - wsp. bezp.).
Rzeczywistą konstrukcję modelujemy powłoką sferyczną opartą na wieńcu i powłoką walcową
zamocowaną w nieodkształcalnym dnie. Wykorzystamy osiową symetrię konstrukcji.
Do rozwiązania zadania użyto element powłoki osiowo--symetrycznej modelując nim
powłokę sferyczną i walcową
(typ konstrukcji ps)
oraz element pierścienia do zamodelowania wieńca (typ konstrukcji pi).
Oba elementy mają takie same stopnie swobody w węźle dlatego możemy łączyć je w jednym zadaniu.
Schemat zadania wprowadzamy w układzie osi XY, pamiętając, że w rzeczywistości
schemat zadania to powłoka otrzymana z obrotu wprowadzonej przez nas łamanej
wokół osi Y. Pojedyńczy element nie jest więc odcinkiem a stożkiem ściętym.
Element pierścienia to w naszym modelu 1 punkt. żeby uniknąć zmniejszenia
konstrukcji a także zmniejszenia bezpieczeństwa, element wieńca umieszczono na przecięciu
powłoki sferycznej i walcowej, które w ten sposób trochę powiększono.
Obciążenie skupione działające w węzłach jest sumą obciążenia
działającego na obwodzie
(jednostka dla sił -- N, dla momentów Nm), obciążenie ciągłe to obciążenie działające
na 1 m2 powierzchni elementu (jednostki dla sił N/m2 dla momentów Nm/m2).
W wyniku obliczeń otrzymujemy przemieszczenia o wartościach identycznych na
całym obwodzie, oraz siły wewnętrzne przypadające na 1m obwodu (jednostki
dla sił -- N/m dla momentów Nm/m). Reakcje otrzymujemy, podobnie jak siły
skupione, zebrane z obwodu.
Ze względu na rodzaj obciążenia oraz sposób uwzględniania go w sytemie, przy
wprowadzaniu go kierujemy się następującymi zasadami:
- Jako ciężar własny rozumiemy ciężar elementów żelbetowych.
W FEASie ciężar własny uwzględniamy poprzez podanie gęstości
materiału Ro[kg/m3],
podanie wymiarów konstrukcji czyli jej objętości V[m3] i
działającego na tę masę przyspieszenia czyli wartości przyspieszenia ziemskiego g[m/s2].
żeby otrzymać siły obciążające konstrukcję mnożymy Ro*g*V=Pc[N].
Jeżeli dane mamy siły objętościowe od ciężaru własnego czyli Ro*g, a tak jest w naszym zadaniu,
możemy dla uniknięcia przeliczeń wpisać jako gęstości wartość tych sił
(25kN/m3), przyjmując
wartość działającego przyspieszenia jako 1 (lub -1 zależnie od
przyjętego układu współrzędnych).
- Obciążenie opisujemy w układzie globalnym (komenda uoe -- układ obciążenia elementowego
pozwala na wybór układu). Układ lokalny byłby niekorzystny ze względu na elementy kopuły.
Każdy z elementów ma inny układ lokalny, a co jest z tym związane, różny opis działającego
obciążenia.
- Obciążenie kopuły realizujemy poprzez zsumowanie obciążenia ciężarem
własnym kopuły żelbetowej, obciążenia ciągłego od obciążenia warstwami
materiałów leżącymi na kopule,
obciążenia śniegiem.
kolejne warstwy leżące na kopule obc.char [kN/m2] gammaf obc.obl. [kN/m2]
warstwa wyrównawcza 0.02m*15kN/m3 0.30 1.3 0.39
wełna mineralna 0.05m*1.0kN/m3 0.05 1.3 0.07
beton na siatce stalowej 0.03*24kN/m3 0.72 1.3 0.94
2 x papa na lepiku 0.10 1.3 0.13
razem obciążenie stałe 1.17 1.53
1.53 kN/m2 jest to wartość obciążenia leżącego na kopule.
Obciążonie śniegiem
dla obiektów zlokalizowanych w pierwszej strefie śniegowej wynosi Qk = 0.7kN/m2.
Współczynnik kształtu dachu C=0.8, współczynnik bezpiczeństwa gammaf=1.4
S = Qk * C * gammaf =0.78 kN/m2.
- Obciążenie wieńca to tylko jego ciężar własny.
- Obciążenie walca to ciężar własny oraz parcie cieczy (p[kN/m2]=gammacieczy[kN/m3]*h[m]), które także musimy opisać oddzielnie dla każdego elementu.
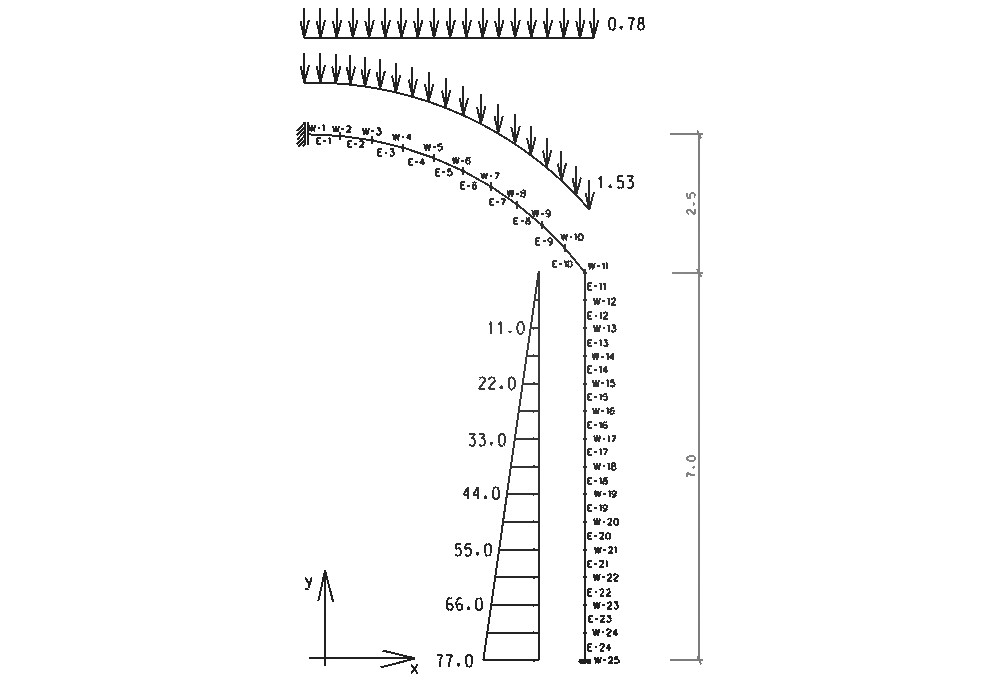
Rys.2. Model konstrukcji.
ROZPOCZĘCIE PRACY.
$ feas - wejście do systemu feas,
FEAS> - system zgłasza gotowość do pracy,
OPIS KONSTRUKCJI.
FEAS> ok
- wejście do podsystemu OK - Opis Konstrukcji,
Podaj rodzaj konstrukcji ps
- ps symbol oznaczający powłokę osiowo-symetryczną,
OK>
węzły i elementy powłoki sferycznej
węzły powłoki sferycznej wprowadzamy w układzie biegunowym r=6.25m,
fi1=90o, fi2=36,87o, środek układu współrzędnych xo=0, yo=0.
OK> w w-1 6.25 90
OK> w w-2 6.25 36.87
OK> gw w-1 w-2 9
OK> zuw w-1 do w-11 0 0
OK> w w-1 5 3.75
OK> w w-11 0 6.25 - węzły w-1 i w-11 mają dokładnie
takie współrzędne, a w wyniku zamiany układu współrzędnych
zostały przypisane im wielkości przybliżone,
OK> e e-1 w-1 w-2
OK> ge e-1 1 1 10 - wygenerowanie 10 elementów pomiędzy węzłami
w-1 i w-11, korzystając z elementu wzorcowego e-1,
węzły i elementy powłoki walcowej
OK> w w-12 5 -3.25
OK> gw w-11 w-12 13
OK> e e-11 w-11 w-12
OK> ge e-11 1 1 14
wczytanie danych materiałowych i geometrycznych
OK> m m1
MAT: Ro=0 ?>25
MAT: E=0 ?> 3e7
MAT: Ni=0 ?> 0.1667
MAT: AlfT=0 ?> 0
OK> g g1
Geom: H=0 > 0.06
OK> g g2
Geom: H=0 > 0.18
OK> pe e-1 do e-10 m1 g1
OK> pe e-11 do e-24 m1 g2
wprowadzenie wieńca
OK> zt pi - zmiana typu elementu na element pierścienia,
OK> e e-25 w-11 - elemet pierścienia opisujemy podając jeden węzeł
tam gdzie pierścień się znajduje, w naszym schemacie jest to węzeł w-11,
OK> g g3
Geom: A=0 > 0.0792
Geom: Jx=0 > 0.3194e-3
Geom: Jy=0 > 0.8554e-3
OK> m m3
MAT: Ro=0 ?> 25
MAT: E=0 ?> 3e7
MAT: AlfT=0 ?> 0
OK> pe e-25 m3 g3
OK> zt ps - aktualny typ konstrukcji to powłoka osiowo--symetryczna,
warunki brzegowe
OK> wb w-1 ux fiz
OK> wb w-25 ux uy fiz
opis obciążenia elementowego
OK> uoe g - przyjmuję globalny układ odniesienia do opisu
wszystkich obciążeń elementowych,
kopuła
OK> oe oe-15 /ln - obciążenie warstwami materiałów leżącymi na kopule,
px1=0 >
py1=0 > -1.53
mz1=0 >
px2=0 >
py2=0 > -1.53
pz2=0 >
OK> pe e-1 do e-10 oe-15
wartość obciążenia śniegiem dziąłającego na poszczególne elementy
jest różna, podamy opis dla jednego elementu e-1, pozostałe należy wprowadzić
analogicznie, wartość obciążenia śniegiem na m2 rzutu wynosi 0.78.
OK> oe o1 /ln
px1=0 >
py1=0 > -0.778 - py=0.78 * (Xk - Xp)/l, gdzie Xk - ozncza
współrzędną x końca elementu, Xp - współrzędna x początku elementu, l -- jego długość,
mz1=0 >
px2=0 >
py2=0 > -0.778
pz2=0 >
OK> pe e-1 o1
walec
obciążenie parciem cieczy należy opisać dla każdego elementu,
pokazany zostanie opis dla elementu e-11, pozostałe opisuje się analogicznie,
wartości obciążenia znajdują się na schemacie,
OK> oe oe-1 /ln
px1=0 > 0
py1=0 >
mz1=0 >
px2=0 > 5.5
py2=0 >
pz2=0 >
OK> pe e-11 oe-1
zapisanie danych do pliku
OK> zap zbiornik - zapisanie danych do zadania w pliku POWCW,
TYTUL> Zbiornik na ciecz -- powłoka osiowo--symetryczna
OK> .. - wyjście z podsystemu OK,
ROZWIĄZANIE ZADANIA
FEAS> ro scw
- rozwiązanie zadania według własnego algorytmu, umieszczonego w pliku SC.ALG,
- spr -- sprawdzenie poprawności wprowadzonych danych,
- st -- utworzenie macierzy sztywności,
- sw -- utworzenie wektora prawych stron,
- cw y -1 -- obliczenie sił węzłowych od obciążenia
ciężarem własnym
i dodanie go do wektora prawych stron,
- rur -- rozwiązanie układu równań,
- nw -- obliczenie naprężeń węzłowych.
Zadanie zostało rozwiązane -- możemy wyświetlić i obejrzeć wyniki. Ważne jest
aby na podstawie analizy wyników wykluczyć rozwiązania błedne, otrzymane
na skutek błędnie wprowadzonych danych.
Pierwszym kryterium oceny wyników jest rysunek konstrukcji odkształconej.
Powinien być on zgodny z naszym wyobrażeniem odkształconej konstrukcji
pod działaniem danego obciążenia. Jeżeli tak nie jest należy sprawdzić układ
opisu obciążenia (standartowo jest lokalny elementowy), oraz przyjęte znaki przy wartościach
obciążenia.
Drugim kryterium jest równowaga obciążenia zewnętrznego z otrzymanymi reakcjami.
Dla powłoki osiowo--symetrycznej możemy analizować tylko równowage sił i reakcji
działających w kierunku osi Y. Sumujemy więc obciążenie pamiętając o tym, że
obciążenie ciągłe działa na 1 m2 (N/m2) powierzchni elementu, natomiast obciążenie
skupione i reakcja jest zebrana z obwodu (N). Przy wielu rodzajach obciążenia zadanie możemy rozwiązywać etapami,
sprawdzając równowagę po każdym dołączonym schemacie obciążenia.
Trzecie kryterium to, przy obciążeniu ciężarem własnym, porównanie orientacyjnego
ciężaru konstrukcji policzonego ręcznie z sumą sił grawitacyjnych
pokazywaną przez system w trakcie rozwiązywania zadania.
W naszym zadaniu suma obciążenia zewnętrznego to
P(ciężar własny) + P(śnieg) + P(ciężar warstw leżących na kopule) =
= 1198.91kN + pi*r2*0.78
+ 2*pi*R*h*1.53 = 1410.144 kN
Jest ona w równowadze z reakcjami (można je wyświetlić w podsystemie WS po
rozwiązaniu zadania).
Otrzymane wyniki to przemieszczenia ux, uy, i fiz (jednostki -- metry i radiany)
oraz siły wewnętrzne. Symbolem Ns oznaczona jest siła działająca w kierunkach
południków sfery i walca, Nt to siła działająca w kierunkach równoleżników
(jednostki to kN/m). Ms to wartości momentów deformujących południki,
Mt to momenty deformujące równoleżniki ( jednostki to kNm/m). Dla wieńca
otrzymujemy siłę rozciągającą go N (kN), oraz moment skręcający Mx (kNm).
Poniżej przedstawiamy wykresy otrzymanych przemieszczeń oraz sił wewnętrznych,
oraz porównanie ich z wartościami liczonymi analitycznie w oparciu o teorię
powłok obrotowych.
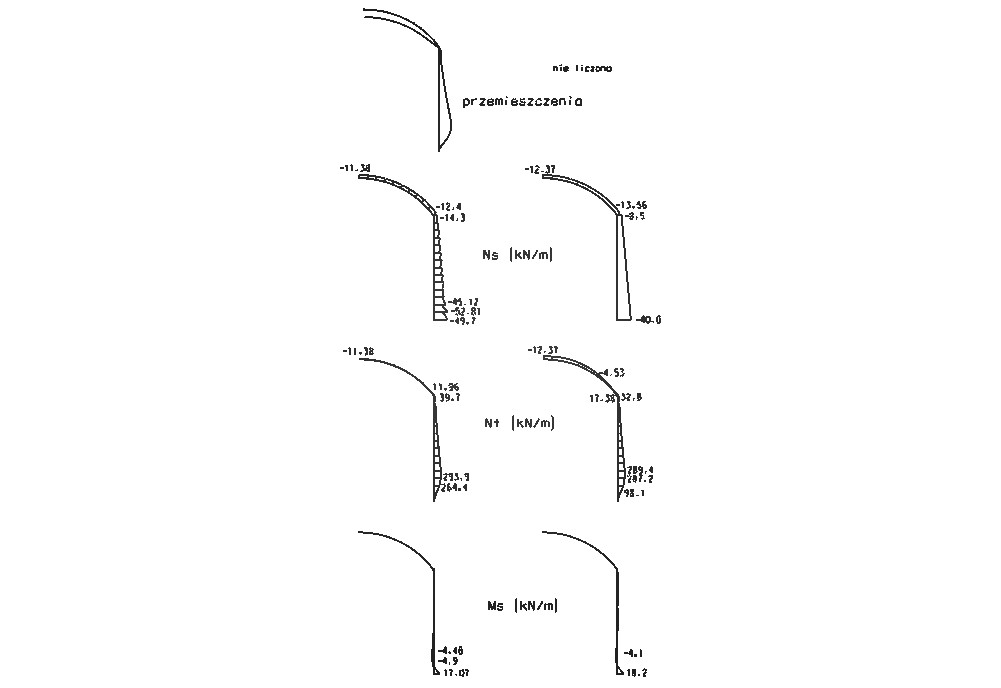
Rys.3. Otrzymane wyniki:
-- w pierwszej kolumnie z wykorzystaniem MES,
-- w drugiej obliczone analitycznie w oparciu o teorię powłok obrotowych.
Dla danego zbiornika wypełnionego wodą znaleźć przemieszczenia oraz siły wewnętrzne.

Rys.1. Zbiornik na wodę.
Dane: beton B-25, E=3107 2kPa, ni=1/6, gammac= 10 kN/m32 * 1.1 = 11kN/m32 (1.1 - wsp. bezp.).
Rzeczywistą konstrukcję modelujemy powłoką sferyczną opartą na wieńcu i powłoką walcową zamocowaną w nieodkształcalnym dnie. Wykorzystamy osiową symetrię konstrukcji. Do rozwiązania zadania użyto element powłoki osiowo--symetrycznej modelując nim powłokę sferyczną i walcową (typ konstrukcji ps) oraz element pierścienia do zamodelowania wieńca (typ konstrukcji pi). Oba elementy mają takie same stopnie swobody w węźle dlatego możemy łączyć je w jednym zadaniu. Schemat zadania wprowadzamy w układzie osi XY, pamiętając, że w rzeczywistości schemat zadania to powłoka otrzymana z obrotu wprowadzonej przez nas łamanej wokół osi Y. Pojedyńczy element nie jest więc odcinkiem a stożkiem ściętym. Element pierścienia to w naszym modelu 1 punkt. żeby uniknąć zmniejszenia konstrukcji a także zmniejszenia bezpieczeństwa, element wieńca umieszczono na przecięciu powłoki sferycznej i walcowej, które w ten sposób trochę powiększono.
Obciążenie skupione działające w węzłach jest sumą obciążenia działającego na obwodzie (jednostka dla sił -- N, dla momentów Nm), obciążenie ciągłe to obciążenie działające na 1 m2 powierzchni elementu (jednostki dla sił N/m2 dla momentów Nm/m2). W wyniku obliczeń otrzymujemy przemieszczenia o wartościach identycznych na całym obwodzie, oraz siły wewnętrzne przypadające na 1m obwodu (jednostki dla sił -- N/m dla momentów Nm/m). Reakcje otrzymujemy, podobnie jak siły skupione, zebrane z obwodu. Ze względu na rodzaj obciążenia oraz sposób uwzględniania go w sytemie, przy wprowadzaniu go kierujemy się następującymi zasadami:
- Jako ciężar własny rozumiemy ciężar elementów żelbetowych. W FEASie ciężar własny uwzględniamy poprzez podanie gęstości materiału Ro[kg/m3], podanie wymiarów konstrukcji czyli jej objętości V[m3] i działającego na tę masę przyspieszenia czyli wartości przyspieszenia ziemskiego g[m/s2]. żeby otrzymać siły obciążające konstrukcję mnożymy Ro*g*V=Pc[N]. Jeżeli dane mamy siły objętościowe od ciężaru własnego czyli Ro*g, a tak jest w naszym zadaniu, możemy dla uniknięcia przeliczeń wpisać jako gęstości wartość tych sił (25kN/m3), przyjmując wartość działającego przyspieszenia jako 1 (lub -1 zależnie od przyjętego układu współrzędnych).
- Obciążenie opisujemy w układzie globalnym (komenda uoe -- układ obciążenia elementowego pozwala na wybór układu). Układ lokalny byłby niekorzystny ze względu na elementy kopuły. Każdy z elementów ma inny układ lokalny, a co jest z tym związane, różny opis działającego obciążenia.
- Obciążenie kopuły realizujemy poprzez zsumowanie obciążenia ciężarem
własnym kopuły żelbetowej, obciążenia ciągłego od obciążenia warstwami
materiałów leżącymi na kopule,
obciążenia śniegiem.
kolejne warstwy leżące na kopule obc.char [kN/m2] gammaf obc.obl. [kN/m2] warstwa wyrównawcza 0.02m*15kN/m3 0.30 1.3 0.39 wełna mineralna 0.05m*1.0kN/m3 0.05 1.3 0.07 beton na siatce stalowej 0.03*24kN/m3 0.72 1.3 0.94 2 x papa na lepiku 0.10 1.3 0.13 razem obciążenie stałe 1.17 1.53
1.53 kN/m2 jest to wartość obciążenia leżącego na kopule.
Obciążonie śniegiem dla obiektów zlokalizowanych w pierwszej strefie śniegowej wynosi Qk = 0.7kN/m2. Współczynnik kształtu dachu C=0.8, współczynnik bezpiczeństwa gammaf=1.4 S = Qk * C * gammaf =0.78 kN/m2. - Obciążenie wieńca to tylko jego ciężar własny.
- Obciążenie walca to ciężar własny oraz parcie cieczy (p[kN/m2]=gammacieczy[kN/m3]*h[m]), które także musimy opisać oddzielnie dla każdego elementu.

Rys.2. Model konstrukcji.
Zadanie zostało rozwiązane -- możemy wyświetlić i obejrzeć wyniki. Ważne jest
aby na podstawie analizy wyników wykluczyć rozwiązania błedne, otrzymane
na skutek błędnie wprowadzonych danych.
Pierwszym kryterium oceny wyników jest rysunek konstrukcji odkształconej.
Powinien być on zgodny z naszym wyobrażeniem odkształconej konstrukcji
pod działaniem danego obciążenia. Jeżeli tak nie jest należy sprawdzić układ
opisu obciążenia (standartowo jest lokalny elementowy), oraz przyjęte znaki przy wartościach
obciążenia.
Drugim kryterium jest równowaga obciążenia zewnętrznego z otrzymanymi reakcjami.
Dla powłoki osiowo--symetrycznej możemy analizować tylko równowage sił i reakcji
działających w kierunku osi Y. Sumujemy więc obciążenie pamiętając o tym, że
obciążenie ciągłe działa na 1 m2 (N/m2) powierzchni elementu, natomiast obciążenie
skupione i reakcja jest zebrana z obwodu (N). Przy wielu rodzajach obciążenia zadanie możemy rozwiązywać etapami,
sprawdzając równowagę po każdym dołączonym schemacie obciążenia.
Trzecie kryterium to, przy obciążeniu ciężarem własnym, porównanie orientacyjnego
ciężaru konstrukcji policzonego ręcznie z sumą sił grawitacyjnych
pokazywaną przez system w trakcie rozwiązywania zadania.
W naszym zadaniu suma obciążenia zewnętrznego to
Otrzymane wyniki to przemieszczenia ux, uy, i fiz (jednostki -- metry i radiany)
oraz siły wewnętrzne. Symbolem Ns oznaczona jest siła działająca w kierunkach
południków sfery i walca, Nt to siła działająca w kierunkach równoleżników
(jednostki to kN/m). Ms to wartości momentów deformujących południki,
Mt to momenty deformujące równoleżniki ( jednostki to kNm/m). Dla wieńca
otrzymujemy siłę rozciągającą go N (kN), oraz moment skręcający Mx (kNm).
Poniżej przedstawiamy wykresy otrzymanych przemieszczeń oraz sił wewnętrznych,
oraz porównanie ich z wartościami liczonymi analitycznie w oparciu o teorię
powłok obrotowych.
Rys.3. Otrzymane wyniki:
-- w pierwszej kolumnie z wykorzystaniem MES,
-- w drugiej obliczone analitycznie w oparciu o teorię powłok obrotowych.
$ feas - wejście do systemu feas,
FEAS> - system zgłasza gotowość do pracy,
FEAS> ok
- wejście do podsystemu OK - Opis Konstrukcji,
Podaj rodzaj konstrukcji ps
- ps symbol oznaczający powłokę osiowo-symetryczną,
OK>
OK> w w-1 6.25 90
OK> w w-2 6.25 36.87
OK> gw w-1 w-2 9
OK> zuw w-1 do w-11 0 0
OK> w w-1 5 3.75
OK> w w-11 0 6.25 - węzły w-1 i w-11 mają dokładnie
takie współrzędne, a w wyniku zamiany układu współrzędnych
zostały przypisane im wielkości przybliżone,
OK> e e-1 w-1 w-2
OK> ge e-1 1 1 10 - wygenerowanie 10 elementów pomiędzy węzłami
w-1 i w-11, korzystając z elementu wzorcowego e-1,
OK> w w-12 5 -3.25
OK> gw w-11 w-12 13
OK> e e-11 w-11 w-12
OK> ge e-11 1 1 14
OK> m m1
MAT: Ro=0 ?>25
MAT: E=0 ?> 3e7
MAT: Ni=0 ?> 0.1667
MAT: AlfT=0 ?> 0
OK> g g1
Geom: H=0 > 0.06
OK> g g2
Geom: H=0 > 0.18
OK> pe e-1 do e-10 m1 g1
OK> pe e-11 do e-24 m1 g2
OK> zt pi - zmiana typu elementu na element pierścienia,
OK> e e-25 w-11 - elemet pierścienia opisujemy podając jeden węzeł
tam gdzie pierścień się znajduje, w naszym schemacie jest to węzeł w-11,
OK> g g3
Geom: A=0 > 0.0792
Geom: Jx=0 > 0.3194e-3
Geom: Jy=0 > 0.8554e-3
OK> m m3
MAT: Ro=0 ?> 25
MAT: E=0 ?> 3e7
MAT: AlfT=0 ?> 0
OK> pe e-25 m3 g3
OK> zt ps - aktualny typ konstrukcji to powłoka osiowo--symetryczna,
OK> wb w-1 ux fiz
OK> wb w-25 ux uy fiz
OK> uoe g - przyjmuję globalny układ odniesienia do opisu
wszystkich obciążeń elementowych,
kopuła
OK> oe oe-15 /ln - obciążenie warstwami materiałów leżącymi na kopule,
px1=0 >
py1=0 > -1.53
mz1=0 >
px2=0 >
py2=0 > -1.53
pz2=0 >
OK> pe e-1 do e-10 oe-15
wartość obciążenia śniegiem dziąłającego na poszczególne elementy
jest różna, podamy opis dla jednego elementu e-1, pozostałe należy wprowadzić
analogicznie, wartość obciążenia śniegiem na m2 rzutu wynosi 0.78.
OK> oe o1 /ln
px1=0 >
py1=0 > -0.778 - py=0.78 * (Xk - Xp)/l, gdzie Xk - ozncza
współrzędną x końca elementu, Xp - współrzędna x początku elementu, l -- jego długość,
mz1=0 >
px2=0 >
py2=0 > -0.778
pz2=0 >
OK> pe e-1 o1
walec
obciążenie parciem cieczy należy opisać dla każdego elementu,
pokazany zostanie opis dla elementu e-11, pozostałe opisuje się analogicznie,
wartości obciążenia znajdują się na schemacie,
OK> oe oe-1 /ln
px1=0 > 0
py1=0 >
mz1=0 >
px2=0 > 5.5
py2=0 >
pz2=0 >
OK> pe e-11 oe-1
OK> zap zbiornik - zapisanie danych do zadania w pliku POWCW,
TYTUL> Zbiornik na ciecz -- powłoka osiowo--symetryczna
OK> .. - wyjście z podsystemu OK,
FEAS> ro scw
- rozwiązanie zadania według własnego algorytmu, umieszczonego w pliku SC.ALG,
P(ciężar własny) + P(śnieg) + P(ciężar warstw leżących na kopule) =
= 1198.91kN + pi*r2*0.78
+ 2*pi*R*h*1.53 = 1410.144 kN
Jest ona w równowadze z reakcjami (można je wyświetlić w podsystemie WS po
rozwiązaniu zadania).
