
ZBIORNIK NA CIECZ PODPARTY SPRĘŻYŚCIE
Znaleźć siły wewnętrzne oraz przemieszczenia w ścianie
cylindrycznego zbiornika opartego na ławie fundamentowej leżącej na sprężystym gruncie.
(zadanie z Konstrukcji żelbetowych t.2 J.Kobiak W.Stachurski str.681
(wydanie z roku 1979). Porównać wyniki z rozwiązaniem otrzymanym przy uwzględnienu
sztywnego podparcia fundamentu.
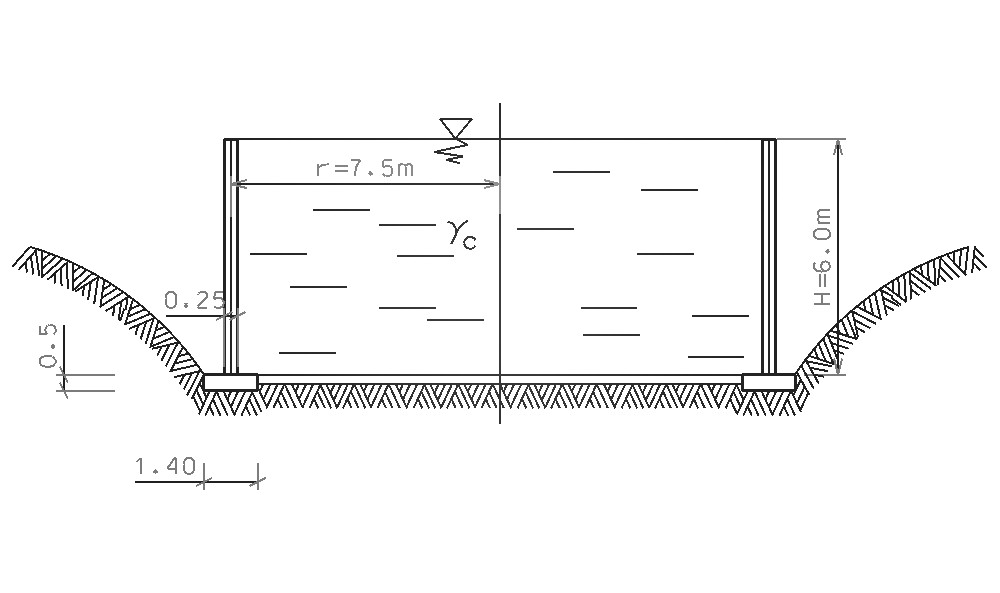
Rys.1. Zbiornik na wodę.
DANE:
H=6.0m -- wysokość sciany,
gamma=10000 N/m3 -- gęstość wody,
Eb=2.3*1010 N/m2, ni=0.1667 -- dane betonu,
C=3*106 N/m3 -- współczynnik podatności gruntu.
Zadanie rozwiązano przyjmując model powłoki osiowo symetrycznej.
Pominięto ciężar własny zbiornika.
Podłoże zamodelowano jako podpory
sprężyste dla których stała sprężystości w kierunku osi y wynosi
ky=C*odległość między podporami*obwód.
Poprawność sprawdzono porównując siły równoleżnikowe z rozwiązaniem
analitycznym oraz analizując przemieszczenia.
Zadanie rozwiązano korzystając z dwóch modeli obliczeniowych, różniących
się sposobem zamodelowania ławy fundamentowej. W pierwszym modelu przyjmujemy
ławę jako powłokę osiowo symetryczną o grubości 0.5m, dzielimy ją
na węzły i elementy, węzły podpieramy sprężyście, wpisując stałą sprężyny
obliczoną zgodnie ze wzorem powyżej. W drugim przypadku ława fundamentowa zamodelowana
została elementem pierścienia, podpartym sprężyście.
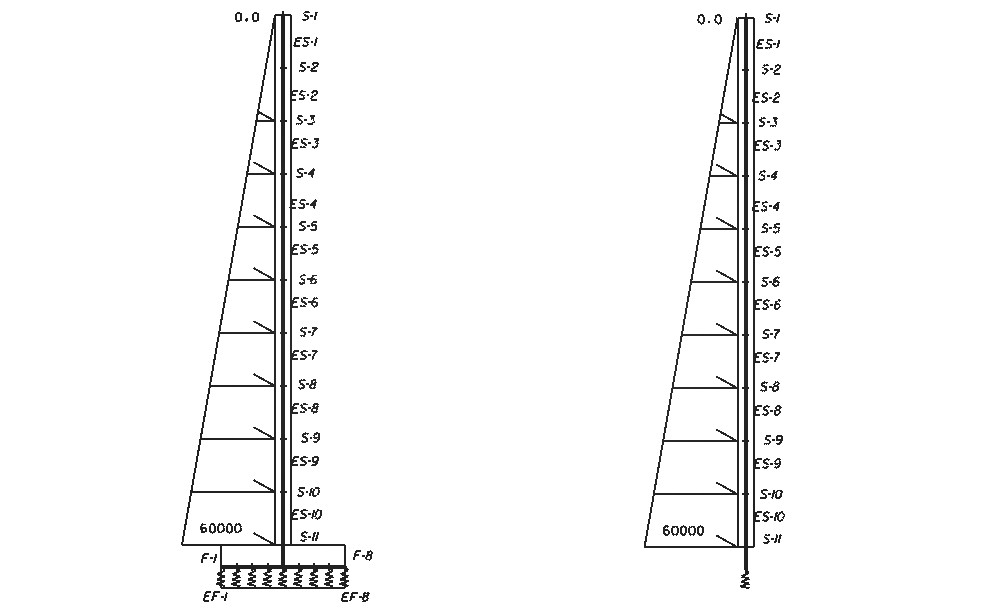
Rys.2. Przyjęte modele, pierwszy z ławą fundamentową zamodelowaną elementami
powłoki osiowo-symetrycznej podpartymi sprężyście, drugi w którym
ława to element pierścienia także podparty sprężyście.
Ze względu na podobny do zadań poprzednich sposób wprowadzania danych poniżej zamieszczono
tylko te fragmenty opisu konstrukcji w systemie FEAS których wprowadzenie
może być kłopotliwe.
Model I.
węzły i elementy
OK>w s-1 7.5 6 - węzeł pierwszy,
OK>w s-11 7.5 0 - węzeł ostatni sciany,
OK>gw s-1 s-11 9 - generacja 9 węzłów posrednich (zwiekszanie
gęstości nie zwiększa znacznie dokładności
wyników tego zadania),
OK>w f-1 6.8 -.25 - węzeł pierwszy fundamentu,
OK>w f-9 8.2 -.25 - węzeł ostatni fundamentu,
OK>gw f-1 f-9 7 - węzły pośrednie,
OK>e es-1 s-1 s-2
OK>ge es-1 1 1 10 - generacja 10 elementów pomiędzy s-1 i s-11
w/g wzoru es-1,
OK>e ef-1 f-1 f-2
OK>ge ef-1 1 1 8
OK>e es-11 s-11 f-5 - element łączący fundament ze ścianą,
dane materiału
OK>m zb
MAT: Ro=0 ?> - gęstość (domyślnie 0),
MAT: E=0 ?> 2.3e10 - współczynnik sprężystości [N/m2],
MAT: Ni=0 ?> .1666667 - współczynnik Poissona,
MAT: AlfT=0 ?> - współczynnik rozszerzalności termicznej,
dane geometryczne
OK>g gs
Geom:H=0?> .25 - grubość ściany,
OK>g gf
Geom:H=0?> .5 - grubość fundamentu,
podpory sprężyste
należy podać węzły podparte sprężyście, oraz wartości stałych sprężystości
działających w kierunkach stopni swobody ( w naszym zadaniu przyjmujemy,
że sprężyste oddziaływanie gruntu związane jest z przemieszczeniem uy).
OK> ps
PS:KX=?,KY=?,KSZ=?> F-1 0 13.525e6
PS:KX=?,KY=?,KSZ=?> F-2 0 26.47e6
PS:KX=?,KY=?,KSZ=?> F-3 0 25.89e6
PS:KX=?,KY=?,KSZ=?> F-4 0 25.32e6
PS:KX=?,KY=?,KSZ=?> F-5 0 24.74e6
PS:KX=?,KY=?,KSZ=?> F-6 0 24.16e6
PS:KX=?,KY=?,KSZ=?> F-7 0 23.59e6
PS:KX=?,KY=?,KSZ=?> F-8 0 23.01e6
PS:KX=?,KY=?,KSZ=?> F-9 0 12.215e6
obciążenie elementowe (opis w układzie elementowym)
OK> oe o1 /ln - obciążenie o nazwie o1 liniowo zmienne(/ln),
px1=0 > 0
py1=0 > 0
mz1=0 > 0
px2=0 > 0
py2=0 > 6000
pz2=0 > 0
Analogicznie wprowadzamy pozostałe obciążenia elementowe, pamiętając o
przyporządkowaniu ich do elementu.
przypisanie elementom parametrów mat. i geom.
OK>pe es-1 do es-11 zb gs
OK>pe ef-1 do ef-8 zb gf
zapamiętanie danych
OK> zap zbiornik - zapisanie danych do pliku ZBIORNIK,
TYTUL> Zbiornik cylindryczny podparty sprezyscie
ROZWIĄZANIE ZADANIA
OK>..
FEAS> ro s
Model II.
Oba zadania różnią się tylko sposobem opisu ławy fundamentowej, poniżej
ta część wprowadzanych danych.
wprowadzenie wieńca
OK> zt pi - zmiana typu elementu na element pierścienia,
OK> e w-1 s-11 - elemet pierścienia opisujemy podając jeden węzeł
tam gdzie pierścień się znajduje, w naszym schemacie jest to węzeł s-11,
OK> g g2
Geom: A=0 > 0.7
Geom: Jx=0 > 0.01458
Geom: Jy=0 > 0.1143
OK> m m2
MAT: Ro=0 ?>
MAT: E=0 ?> 2.3e10
MAT: AlfT=0 ?> 0
OK> pe w-1 m2 g2
OK> zt ps - aktualny typ konstrukcji to powłoka osiowo--symetryczna,
podpory sprężyste
OK> ps
PS:KX=?,KY=?,KSZ=?> s-11 0 197.92e6
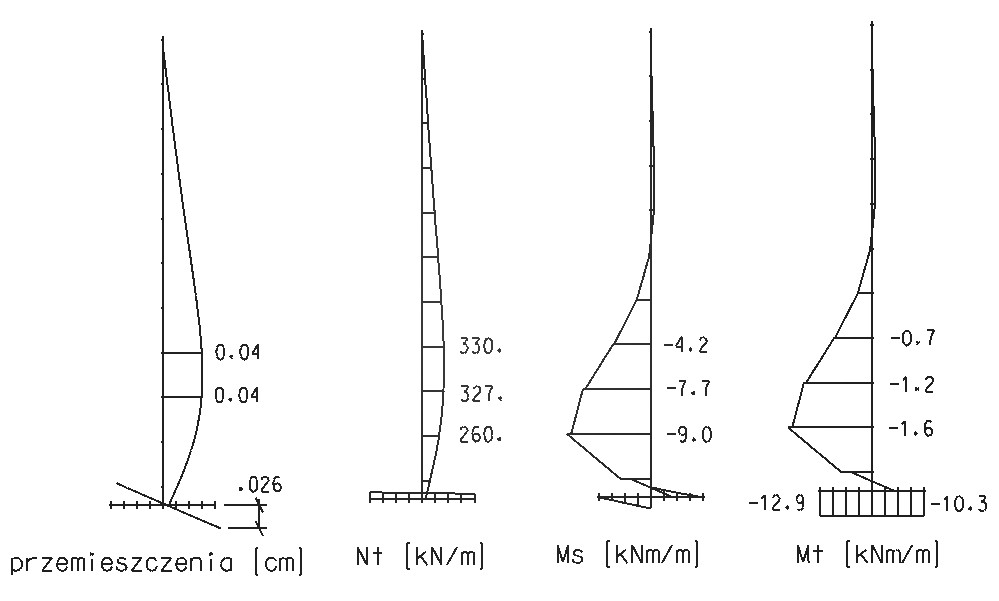
Rys.3. Wyniki otrzymane dla modelu pierwszego.
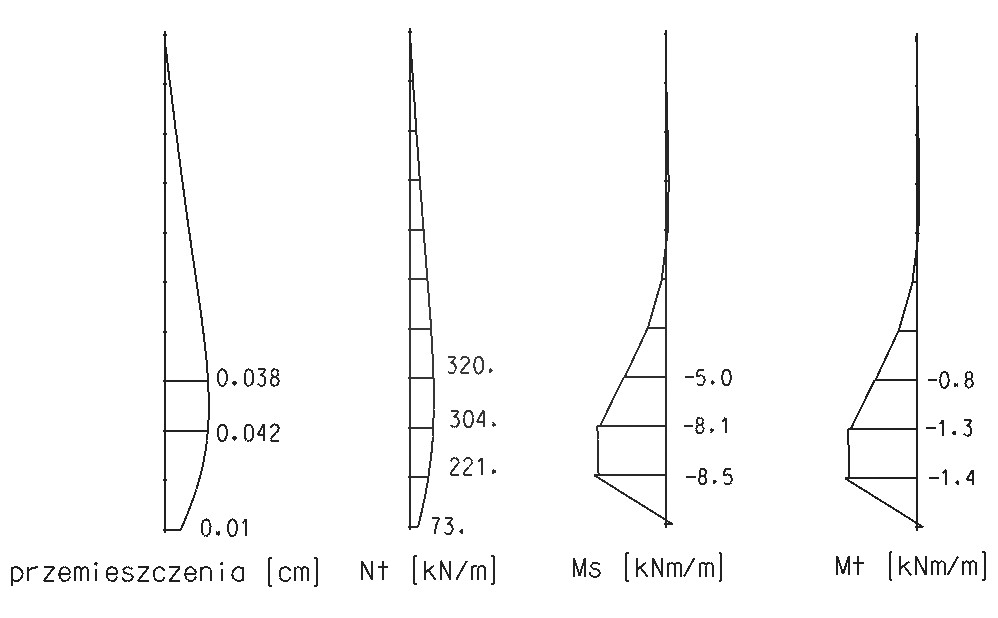
Rys.4. Wyniki otrzymane dla modelu drugiego.
Znaleźć siły wewnętrzne oraz przemieszczenia w ścianie cylindrycznego zbiornika opartego na ławie fundamentowej leżącej na sprężystym gruncie. (zadanie z Konstrukcji żelbetowych t.2 J.Kobiak W.Stachurski str.681 (wydanie z roku 1979). Porównać wyniki z rozwiązaniem otrzymanym przy uwzględnienu sztywnego podparcia fundamentu.

Rys.1. Zbiornik na wodę.
DANE: H=6.0m -- wysokość sciany, gamma=10000 N/m3 -- gęstość wody, Eb=2.3*1010 N/m2, ni=0.1667 -- dane betonu, C=3*106 N/m3 -- współczynnik podatności gruntu.
Zadanie rozwiązano przyjmując model powłoki osiowo symetrycznej. Pominięto ciężar własny zbiornika. Podłoże zamodelowano jako podpory sprężyste dla których stała sprężystości w kierunku osi y wynosi ky=C*odległość między podporami*obwód. Poprawność sprawdzono porównując siły równoleżnikowe z rozwiązaniem analitycznym oraz analizując przemieszczenia. Zadanie rozwiązano korzystając z dwóch modeli obliczeniowych, różniących się sposobem zamodelowania ławy fundamentowej. W pierwszym modelu przyjmujemy ławę jako powłokę osiowo symetryczną o grubości 0.5m, dzielimy ją na węzły i elementy, węzły podpieramy sprężyście, wpisując stałą sprężyny obliczoną zgodnie ze wzorem powyżej. W drugim przypadku ława fundamentowa zamodelowana została elementem pierścienia, podpartym sprężyście.

Rys.2. Przyjęte modele, pierwszy z ławą fundamentową zamodelowaną elementami powłoki osiowo-symetrycznej podpartymi sprężyście, drugi w którym ława to element pierścienia także podparty sprężyście.
Ze względu na podobny do zadań poprzednich sposób wprowadzania danych poniżej zamieszczono tylko te fragmenty opisu konstrukcji w systemie FEAS których wprowadzenie może być kłopotliwe.
Model I.
| OK>w s-1 7.5 6 | - węzeł pierwszy, |
| OK>w s-11 7.5 0 | - węzeł ostatni sciany, |
| OK>gw s-1 s-11 9 | - generacja 9 węzłów posrednich (zwiekszanie gęstości nie zwiększa znacznie dokładności wyników tego zadania), |
| OK>w f-1 6.8 -.25 | - węzeł pierwszy fundamentu, |
| OK>w f-9 8.2 -.25 | - węzeł ostatni fundamentu, |
| OK>gw f-1 f-9 7 | - węzły pośrednie, |
| OK>e es-1 s-1 s-2 | |
| OK>ge es-1 1 1 10 | - generacja 10 elementów pomiędzy s-1 i s-11 w/g wzoru es-1, |
| OK>e ef-1 f-1 f-2 | |
| OK>ge ef-1 1 1 8 | |
| OK>e es-11 s-11 f-5 | - element łączący fundament ze ścianą, |
| OK>m zb | |
| MAT: Ro=0 ?> | - gęstość (domyślnie 0), |
| MAT: E=0 ?> 2.3e10 | - współczynnik sprężystości [N/m2], |
| MAT: Ni=0 ?> .1666667 | - współczynnik Poissona, |
| MAT: AlfT=0 ?> | - współczynnik rozszerzalności termicznej, |
| OK>g gs | |
| Geom:H=0?> .25 | - grubość ściany, |
| OK>g gf | |
| Geom:H=0?> .5 | - grubość fundamentu, |
należy podać węzły podparte sprężyście, oraz wartości stałych sprężystości działających w kierunkach stopni swobody ( w naszym zadaniu przyjmujemy, że sprężyste oddziaływanie gruntu związane jest z przemieszczeniem uy).
| OK> ps |
| PS:KX=?,KY=?,KSZ=?> F-1 0 13.525e6 |
| PS:KX=?,KY=?,KSZ=?> F-2 0 26.47e6 |
| PS:KX=?,KY=?,KSZ=?> F-3 0 25.89e6 |
| PS:KX=?,KY=?,KSZ=?> F-4 0 25.32e6 |
| PS:KX=?,KY=?,KSZ=?> F-5 0 24.74e6 |
| PS:KX=?,KY=?,KSZ=?> F-6 0 24.16e6 |
| PS:KX=?,KY=?,KSZ=?> F-7 0 23.59e6 |
| PS:KX=?,KY=?,KSZ=?> F-8 0 23.01e6 |
| PS:KX=?,KY=?,KSZ=?> F-9 0 12.215e6 |
| OK> oe o1 /ln | - obciążenie o nazwie o1 liniowo zmienne(/ln), |
| px1=0 > 0 | |
| py1=0 > 0 | |
| mz1=0 > 0 | |
| px2=0 > 0 | |
| py2=0 > 6000 | |
| pz2=0 > 0 |
Analogicznie wprowadzamy pozostałe obciążenia elementowe, pamiętając o
przyporządkowaniu ich do elementu.
Rys.3. Wyniki otrzymane dla modelu pierwszego.
Rys.4. Wyniki otrzymane dla modelu drugiego.
OK>pe es-1 do es-11 zb gs
OK>pe ef-1 do ef-8 zb gf
OK> zap zbiornik - zapisanie danych do pliku ZBIORNIK,
TYTUL> Zbiornik cylindryczny podparty sprezyscie
OK>..
FEAS> ro s
Model II.
Oba zadania różnią się tylko sposobem opisu ławy fundamentowej, poniżej
ta część wprowadzanych danych.
OK> zt pi - zmiana typu elementu na element pierścienia,
OK> e w-1 s-11 - elemet pierścienia opisujemy podając jeden węzeł
tam gdzie pierścień się znajduje, w naszym schemacie jest to węzeł s-11,
OK> g g2
Geom: A=0 > 0.7
Geom: Jx=0 > 0.01458
Geom: Jy=0 > 0.1143
OK> m m2
MAT: Ro=0 ?>
MAT: E=0 ?> 2.3e10
MAT: AlfT=0 ?> 0
OK> pe w-1 m2 g2
OK> zt ps - aktualny typ konstrukcji to powłoka osiowo--symetryczna,
OK> ps
PS:KX=?,KY=?,KSZ=?> s-11 0 197.92e6

