
DRGANIA BUDYNKU WYSOKIEGO
Dla budynku wysokiego 14 kondygnacyjnego znaleźć czestości drgań własnych.
Modelem obliczeniowym budynku jest rama przestrzenna składająca się z
sześciu ram płaskich połączonych ze sobą podciągami. Obciążenie to
ciężar własny konstrukcji ( rama, ściany i stropy) oraz obciążenie użytkowe.

Rys.1. Schemat konstrukcji.
Budynek wysoki jest konstrukcją przestrzenną. Przyjmując model ramy przestrzennej
najlepiej przedstawilibyśmy rzeczywistą konstrukcję jednak model zadania byłby duży,
wiele danych i wyników.
W celu uproszczenia
zakładamy, że
konstrukcja pracuje w jednym kierunku (pracują ramy płaskie), a podciągi
stanowią tylko element konstrukcyjny. Analizowany więc będzie model ramy płaskiej.
Ten budynek wysoki jest tak skonstruowany, że głównym elementem nośnym jest
trzon budynku do którego podwieszone są na linach stropy kolejnych kondygnacji.
Zamodelowanie takiej konstrukcji jest kłopotliwe ze względu na elementy lin. Liny są jakby
elementami prętowymi ale o specyficznym sposobie pracy. Pracują gdy są rozciągane,
a stają się bezużyteczne w przypadku ściskania, nie pracują też na zginanie.
Wprowadzając do modelu linę jako element prętowy musimy uważać, żebu nie wystąpiły
siły ściskające. W przypadku gdy lina jest ściskana musimy ją wyeliminować z modelu.
Element liny nie może też pracować na zginanie. Taki efekt łatwo jest uzyskać
przypisując elementom lin bardzo mały (w porównaniu z rzeczywistym) moment
bezwładności na zginanie.
Problem jak uwzględniać pracę lin w przypadku
dynamiki jest bardziej złożony. Postać z jaką konstrukcja drga powoduje
rozciąganie lin raz z jednej, raz z drugiej strony konstrukcji, elementy linowe mogą być
ściskane. Dlatego w dalszej części przeanalizowano kilka modeli (także ten z linami)
oraz porównano otrzymane wyniki.
W problemach dynamiki działające obciążenie, ciężar własny czy obc.
użytkowe ma wpływ na podatność konstrukcji na drgania. Obciążenie takie w modelu
przedstawiamy jako ciężar własny (na podstawie gęstości materiału i wymiarów elementów
odpowiednio budowana jest macierz mas) lub
jako masy skupione. Masy skupione są to masy równoważące działające
obciążenie (wyrażone w kg) wpływające na bezwładność konstrukcji
przy ruchu w kierunkach X i Y. Nie uwzględniamy wpływu masy na bezwładność obrotową.
Obciążenia skupione i ciągłe modelujemy masami umieszczonymi w węzłach.
Dlatego gęstszy podział na węzły elemntów z występującym obciążeniem ciągłym,
i bardziej równomierny rozkład mas skupionych lepiej przedstawi rzeczywistą pracę konstrukcji.
W przypadku, gdy obciążenia działające w konstrukcji powodują
powstanie dużych sił osiowych ( a tak jest w naszym zadaniu) można
uwzględnić ich wpływ na podatność konstrukcji na drgania. W algorytmie MES
polega to na zbudowaniu dodatku do macierzy sztywności (mac. geometrycznej)
zależnej od występujących sił
osiowych. Przy siłach osiowych dążących do obciążenia krytycznego
(powodującego
wyboczenie) wpływ tych sił będzie widoczny, w innych przypadkach różnice w otrzymanych wynikach będą
minimalne.
Szukając częstości drgań konstrukcji uwzględniamy wpływ ciężaru własnego
na bezwładność konstrukcji
automatycznie przy budowie mac. mas (podajemy niezerową gęstość) lub
zastępujemy go masami skupionymi,
pozostałe rodzaje obciążenia modelujemy jako masy skupione.
Dodatkowo chcąc
uwzględnić działanie dużych sił osiowych wprowadzamy działające obciążenie
jako siły skupione lub obc. ciągłe.
Obliczenia przeprowadzono dla kilku modeli obliczeniowych w celu porównania
otrzymanych wyników, oraz przedstawienia sposobów modelowania.
Geometria
konstrukcji, podział na węzły i elementy, dane materiałowo geometryczne
są podobne we wszystkich wariantach, opis ich pominięto.
Przyjęto następujące dane:
- materiał -- stal o następujących właściwościach E=2.1*1011 N/m2,
Ro (gęstość materiału) =7850 kg/m3,
- geometria elementów:
- słupy (elementy pionowe) A=0.016m2, Jz=0.00022m4,
- rygle (elementy poziome) A=0.01356m2, Jz=0.0001417m4,
- skratowanie wewnątrz środkowego przęsła A=0.0034m2, Jz=0.000053m4,
- liny o przekroju A=0.0054m2.
- Obciążenie dla uproszczenia przyjęto jednakowe na wszystkich kondygnacjach
wynoszące 31.33 kN/m, w sumie na każdej kondygnacji 470.0 kN.
Po odjęciu ciężaru własnego działające obciążenie na kondygnacjach wynosi
442998.33 N, na ostatnie kondygnacji 446064.0 N.
Przykładowe wprowadzenie masy skupionej w węźle w-2 o wartości 5000kg.
OK> ms w-2 5000 5000 - bezwładność w kierunku osi X
Bx=5000kg, bezwładność w kierunku osi Y By=5000kg, bezwładność
obrotowa Jz=0.
W systemie FEAS algorytm obliczania trzech pierwszych częstości drgań
własnych oraz odpowiadających im postaci drgań nosi nazwę dw.
Wywołanie tego algorytmu:
FEAS> ro dw - rozwiązanie zadania (drgania własne).}
Algorytm uwzględniający działanie dużych sił osiowych przy obliczaniu
częstości drgań to
dwo.
FEAS> ro dwo - rozwiązanie zadania (drgania własne konstrukcji obciążonej).
Poniżej analizowane modele oraz wyniki otrzymane dla każdego z nich, czyli trzy
pierwsze częstości drgań oraz odpowiadające im postacie drgań.
1.Rama płaska, model z linami, podział na węzły i elementy zgodny z geometrią
konstrukcji zagęszczony w elementach obciążonych ciągle (rygle),
obciążona ciężarem własnym konstrukcji oraz obc. użytkowym.
Obciążenie to przedstawiono sumarycznie jako obciążenie ciągłe i przyłożono je
w postaci mas skupionych do węzłów elementów poziomych (rygli).
Elementy przyjęto
jako nieważkie Ro=0. W sumie każda
kondygnacja obciążona jest masą 47000kg równoważącą działające
obciążenie.
Elementy lin zamodelowano elementami prętowymi o przekroju
A=0.0054m2 i bardzo małej (w porównaniu z innymi elementami) bezwładności
na zginanie Jz=$1.0*10^{-10}m4. Tak przyjęty model dopuszcza ściskanie elementów lin.

Rys.2. Przyjęty model oraz rozkład mas i sił na kondygnacji.
Otrzymane wyniki

Rys.3. Postacie oraz częstości drgań własnych, omega1 = 2.0336Hz ,omega2 = 6.3629Hz, omega3 = 9.2527Hz
2. Rama płaska, model bez lin, podział na węzły i elementy zgodny z geometrią
konstrukcji zagęszczony w elementach obciążonych ciągle (rygle),
obciążona ciężarem własnym konstrukcji oraz obc. użytkowym.
Ciężar własny i pozostałe obciążenie
zastąpiono masami skupionymi
przyłożonymi do węzłów elementów poziomych (rygli.) Uwzględniono wpływ
sił osiowych na podatność konstrukcji na drgania. Siły przyłożono
do węzłów trzonu konstrukcji.

Rys.4. Przyjęty model oraz rozkład mas i sił na kondygnacji.
Otrzymane wyniki

Rys.5. Postacie oraz częstości drgań własnych, omega1 = 2.0247Hz, omega2 = 6.3014Hz, omega3 = 8.9880Hz.
3. Rama płaska, model bez lin, podział na węzły i elementy zgodny z geometrią
konstrukcji zagęszczony w elementach obciążonych ciągle (rygle),
obciążona ciężarem własnym konstrukcji oraz obc. użytkowym.
Ciężar własny i pozostałe obciążenie
zastąpiono masami skupionymi
przyłożonymi do węzłów elementów poziomych (rygli.)

Rys.6. Przyjęty model oraz rozkład mas na kondygnacji.
Otrzymane wyniki

Rys.7. Postacie oraz częstości drgań własnych, omega1 = 2.1003Hz, omega2 = 6.4071Hz, omega3 = 9.0396Hz.
4. Rama płaska (bez lin), podział na węzły i elementy zgodny z geometrią
konstrukcji,
obciążona ciężarem własnym konstrukcji oraz obc. użytkowym.
Obciążenie to przedstawiono sumarycznie jako obciążenie ciągłe i przyłożono je
w postaci mas skupionych do węzłów elementów poziomych (rygli). W sumie
wartość przyłożonej masy 47000kg co równoważy działające obciążenie.
Elementy przyjęto
jako nieważkie Ro=0.

Rys.8. Przyjęty model oraz rozkład mas na kondygnacji.
Otrzymane wyniki

Rys.9. Postacie oraz częstości drgań własnych, omega1 = 2.0920Hz omega2 = 5.9232Hz omega3 = 7.0130Hz
5. Rama płaska, model bez lin, podział na węzły i elementy zgodny z geometrią
konstrukcji,
obciążona ciężarem własnym konstrukcji oraz obc. użytkowym.
Ciężar własny uwzględniono poprzez podanie Ro=7850 kg/m3, pozostałe
obciążenie zastąpiono masami skupionymi
przyłożonymi do węzłów elementów poziomych (rygli.) Ciężar pojedyńczej kondygnacji
wynosi 2700.167kg, pzostała wartość to 44299.84kg, dla ostatniej kondygnacji
odpowiednio 2393.523kg i 44606.477kg.

Rys.10. Przyjęty model oraz rozkład mas na kondygnacji.
Otrzymane wyniki

Rys.11. Postacie oraz częstości drgań własnych, omega1 = 2.0951Hz omega2 = 6.0065Hz omega3 = 7.2047Hz
6. Rama płaska (bez lin), model konstrukcji ograniczono do trzonu
podział na węzły i elementy zgodny z geometrią
konstrukcji,
obciążona ciężarem własnym konstrukcji oraz obc. użytkowym.
Obciążenie to przedstawiono sumarycznie jako obciążenie ciągłe i przyłożono je
w postaci mas skupionych do węzłów elementów poziomych (rygli).
Obciążenie przyłożono do trzonu konstrukcji.
Elementy przyjęto
jako nieważkie Ro=0.
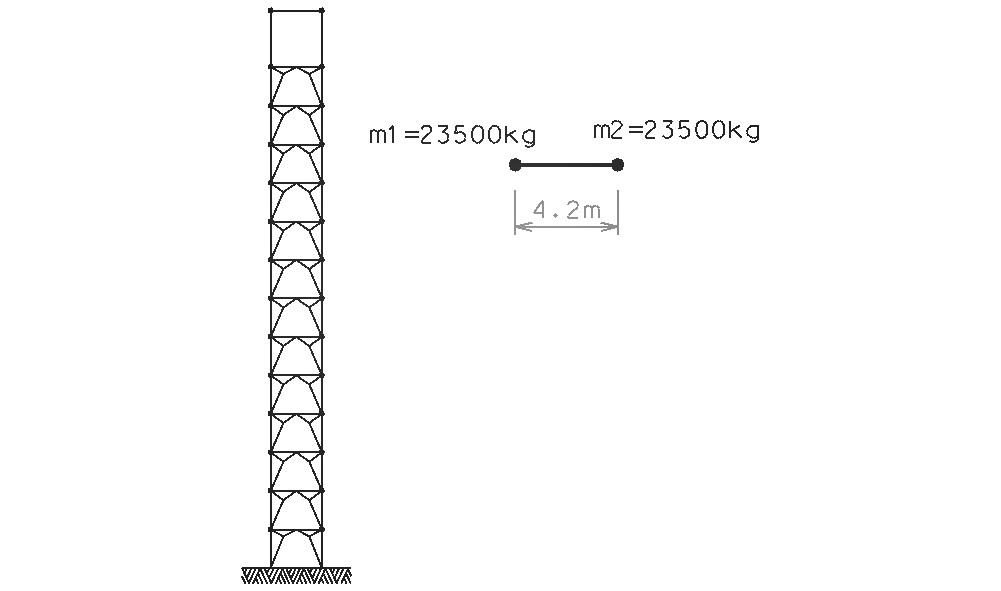
Rys.12. Przyjęty model oraz rozkład mas na kondygnacji.
Otrzymane wyniki
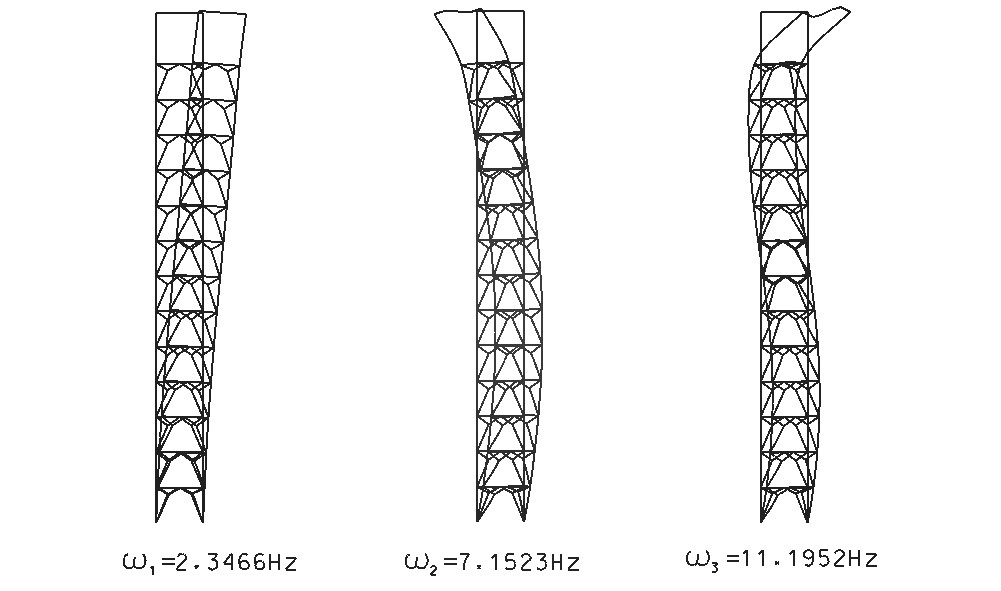
Rys.13. Postacie oraz częstości drgań własnych, omega1 = 2.3466Hz omega2 = 7.1523Hz omega3 = 11.1952Hz.
7. Rama płaska zamodelowana jako wspornik, podział na elementy zgodny z geometrią
konstrukcji, jeden element to jedna kondygnacja,
obciążenie sumacyjne przyłożono w postaci mas skupionych w węzłach modelu.
Wartość bezwładności w kierunku osi x Bx=47000kg, w kierunku osi y By=47000,
bezwładność obrotowa Jz=0.0.
Dane geometryczne, pole przekroju oraz moment bezwładności na zginanie,
obliczono dla przekroju złożonego z dwóch elementów słupów (dwie rury
czworościenne) rozsuniętych na odległość 4.2m (taką, jaki jest rozstaw
słupów).
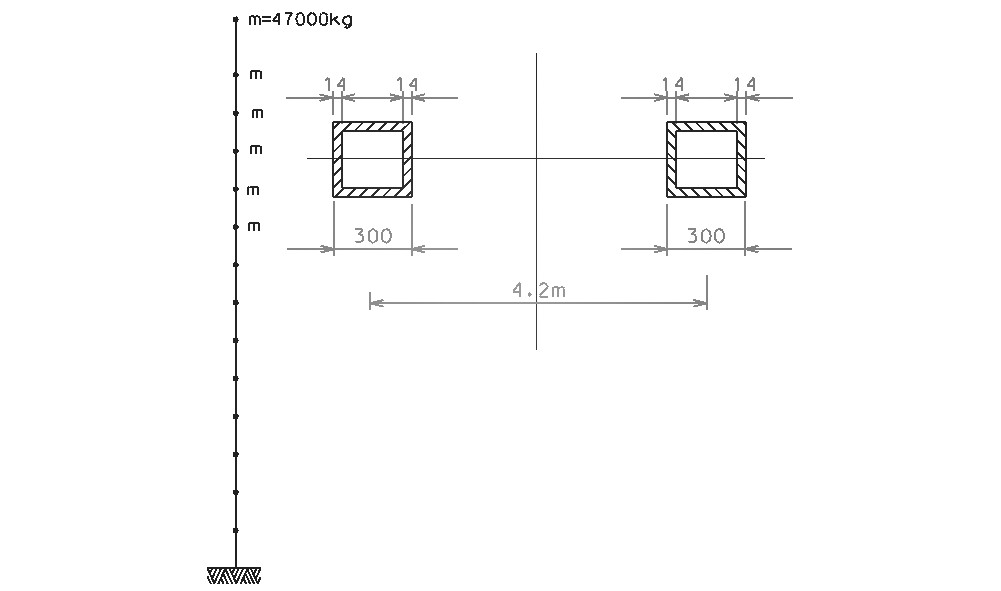
Rys.14. Przyjęty model oraz przyjęty przekrój elementów.
Otrzymane wyniki
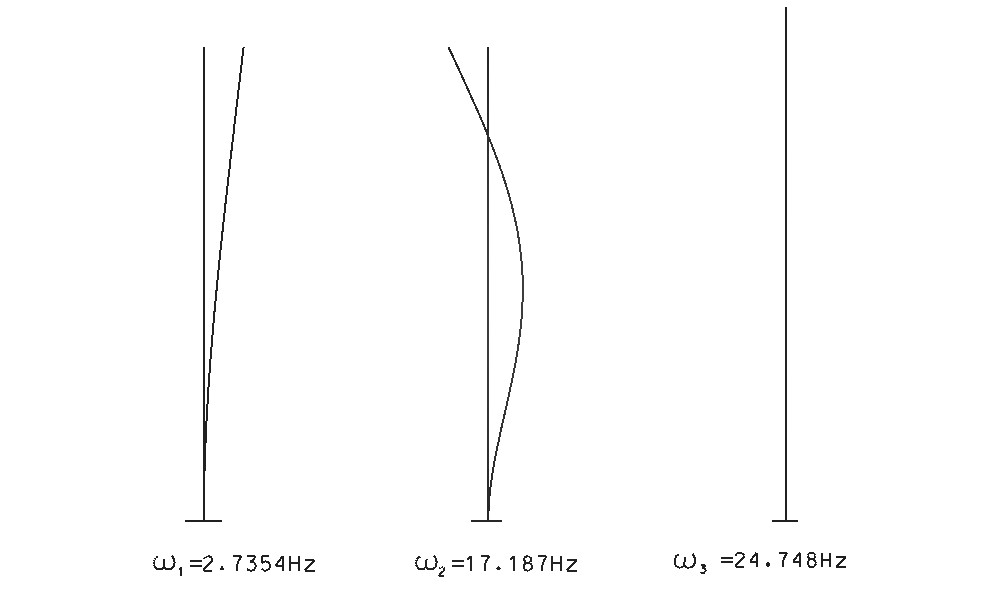
Rys.15. Postacie oraz częstości drgań własnych, omega1 = 2.7354Hz omega2 = 17.187Hz omega3 = 24.748Hz.
Zestawienie przyjętych modeli i otrzymanych wyników.
Przyjęty model omega1[Hz] omega2[Hz] omega3[Hz]
1. Rama płaska, model z linami
gęsty rozkład mas na elementach poziomych,
pręty nieważkie -- całkowite obciążenie zastąpione masami skupionymi,
uwzględniony wpływ sił osiowych w elementach.
2.0336 6.3629 9.2527
2. Rama płaska, model bez lin
gęsty rozkład mas na elementach poziomych,
pręty nieważkie -- całkowite obciążenie zastąpione masami skupionymi,
uwzględniony wpływ sił osiowych w elementach. 2.0247 6.3014 8.9880
3. Rama płaska, model bez lin
gęsty rozkład mas na elementach poziomych,
pręty nieważkie -- całkowite obciążenie zastąpione masami skupionymi,
2.1003 6.4071 9.0396
4. Rama płaska, model bez lin
rzadki rozkład mas na elementach poziomych,
pręty nieważkie -- całkowite obciążenie zastąpione masami skupionymi, 2.0920 5.9232 7.0130
5. Rama płaska, model bez lin
rzadki rozkład mas na elementach poziomych,
masa modelu uwzględnina poprzez podanie gęstości i wymiarów elementów,
pozostałe obciążenie zastąpione masami skupionymi, 2.0951 6.0065 7.2047
6. Rama płaska, model -- sam trzon budynku
pręty nieważkie -- całkowite obciążenie zastąpione masami skupionymi
przyłożonymi
do dwóch węzłów na każdej kondygnacji, 2.3466 7.1523 11.1952
7. Rama płaska, model -- wspornik
pręty nieważkie -- całkowite obciążenie zastąpione masami skupionymi
przyłożonymi
do węzła na poziomie każdej kondygnacji, 2.7354 17.187 24.748
Dla budynku wysokiego 14 kondygnacyjnego znaleźć czestości drgań własnych. Modelem obliczeniowym budynku jest rama przestrzenna składająca się z sześciu ram płaskich połączonych ze sobą podciągami. Obciążenie to ciężar własny konstrukcji ( rama, ściany i stropy) oraz obciążenie użytkowe.

Rys.1. Schemat konstrukcji.
Budynek wysoki jest konstrukcją przestrzenną. Przyjmując model ramy przestrzennej najlepiej przedstawilibyśmy rzeczywistą konstrukcję jednak model zadania byłby duży, wiele danych i wyników. W celu uproszczenia zakładamy, że konstrukcja pracuje w jednym kierunku (pracują ramy płaskie), a podciągi stanowią tylko element konstrukcyjny. Analizowany więc będzie model ramy płaskiej.
Ten budynek wysoki jest tak skonstruowany, że głównym elementem nośnym jest trzon budynku do którego podwieszone są na linach stropy kolejnych kondygnacji. Zamodelowanie takiej konstrukcji jest kłopotliwe ze względu na elementy lin. Liny są jakby elementami prętowymi ale o specyficznym sposobie pracy. Pracują gdy są rozciągane, a stają się bezużyteczne w przypadku ściskania, nie pracują też na zginanie. Wprowadzając do modelu linę jako element prętowy musimy uważać, żebu nie wystąpiły siły ściskające. W przypadku gdy lina jest ściskana musimy ją wyeliminować z modelu. Element liny nie może też pracować na zginanie. Taki efekt łatwo jest uzyskać przypisując elementom lin bardzo mały (w porównaniu z rzeczywistym) moment bezwładności na zginanie.
Problem jak uwzględniać pracę lin w przypadku dynamiki jest bardziej złożony. Postać z jaką konstrukcja drga powoduje rozciąganie lin raz z jednej, raz z drugiej strony konstrukcji, elementy linowe mogą być ściskane. Dlatego w dalszej części przeanalizowano kilka modeli (także ten z linami) oraz porównano otrzymane wyniki.
W problemach dynamiki działające obciążenie, ciężar własny czy obc. użytkowe ma wpływ na podatność konstrukcji na drgania. Obciążenie takie w modelu przedstawiamy jako ciężar własny (na podstawie gęstości materiału i wymiarów elementów odpowiednio budowana jest macierz mas) lub jako masy skupione. Masy skupione są to masy równoważące działające obciążenie (wyrażone w kg) wpływające na bezwładność konstrukcji przy ruchu w kierunkach X i Y. Nie uwzględniamy wpływu masy na bezwładność obrotową. Obciążenia skupione i ciągłe modelujemy masami umieszczonymi w węzłach. Dlatego gęstszy podział na węzły elemntów z występującym obciążeniem ciągłym, i bardziej równomierny rozkład mas skupionych lepiej przedstawi rzeczywistą pracę konstrukcji.
W przypadku, gdy obciążenia działające w konstrukcji powodują powstanie dużych sił osiowych ( a tak jest w naszym zadaniu) można uwzględnić ich wpływ na podatność konstrukcji na drgania. W algorytmie MES polega to na zbudowaniu dodatku do macierzy sztywności (mac. geometrycznej) zależnej od występujących sił osiowych. Przy siłach osiowych dążących do obciążenia krytycznego (powodującego wyboczenie) wpływ tych sił będzie widoczny, w innych przypadkach różnice w otrzymanych wynikach będą minimalne.
Szukając częstości drgań konstrukcji uwzględniamy wpływ ciężaru własnego na bezwładność konstrukcji automatycznie przy budowie mac. mas (podajemy niezerową gęstość) lub zastępujemy go masami skupionymi, pozostałe rodzaje obciążenia modelujemy jako masy skupione. Dodatkowo chcąc uwzględnić działanie dużych sił osiowych wprowadzamy działające obciążenie jako siły skupione lub obc. ciągłe. Obliczenia przeprowadzono dla kilku modeli obliczeniowych w celu porównania otrzymanych wyników, oraz przedstawienia sposobów modelowania. Geometria konstrukcji, podział na węzły i elementy, dane materiałowo geometryczne są podobne we wszystkich wariantach, opis ich pominięto.
Przyjęto następujące dane:
- materiał -- stal o następujących właściwościach E=2.1*1011 N/m2, Ro (gęstość materiału) =7850 kg/m3,
- geometria elementów:
- słupy (elementy pionowe) A=0.016m2, Jz=0.00022m4,
- rygle (elementy poziome) A=0.01356m2, Jz=0.0001417m4,
- skratowanie wewnątrz środkowego przęsła A=0.0034m2, Jz=0.000053m4,
- liny o przekroju A=0.0054m2.
- Obciążenie dla uproszczenia przyjęto jednakowe na wszystkich kondygnacjach wynoszące 31.33 kN/m, w sumie na każdej kondygnacji 470.0 kN. Po odjęciu ciężaru własnego działające obciążenie na kondygnacjach wynosi 442998.33 N, na ostatnie kondygnacji 446064.0 N.
Przykładowe wprowadzenie masy skupionej w węźle w-2 o wartości 5000kg.
| OK> ms w-2 5000 5000 | - bezwładność w kierunku osi X Bx=5000kg, bezwładność w kierunku osi Y By=5000kg, bezwładność obrotowa Jz=0. |
W systemie FEAS algorytm obliczania trzech pierwszych częstości drgań własnych oraz odpowiadających im postaci drgań nosi nazwę dw. Wywołanie tego algorytmu:
| FEAS> ro dw | - rozwiązanie zadania (drgania własne).} |
Algorytm uwzględniający działanie dużych sił osiowych przy obliczaniu częstości drgań to dwo.
| FEAS> ro dwo | - rozwiązanie zadania (drgania własne konstrukcji obciążonej). |
Poniżej analizowane modele oraz wyniki otrzymane dla każdego z nich, czyli trzy pierwsze częstości drgań oraz odpowiadające im postacie drgań.
1.Rama płaska, model z linami, podział na węzły i elementy zgodny z geometrią konstrukcji zagęszczony w elementach obciążonych ciągle (rygle), obciążona ciężarem własnym konstrukcji oraz obc. użytkowym.
Obciążenie to przedstawiono sumarycznie jako obciążenie ciągłe i przyłożono je w postaci mas skupionych do węzłów elementów poziomych (rygli). Elementy przyjęto jako nieważkie Ro=0. W sumie każda kondygnacja obciążona jest masą 47000kg równoważącą działające obciążenie. Elementy lin zamodelowano elementami prętowymi o przekroju A=0.0054m2 i bardzo małej (w porównaniu z innymi elementami) bezwładności na zginanie Jz=$1.0*10^{-10}m4. Tak przyjęty model dopuszcza ściskanie elementów lin.
Rys.2. Przyjęty model oraz rozkład mas i sił na kondygnacji.
Otrzymane wyniki

Rys.3. Postacie oraz częstości drgań własnych, omega1 = 2.0336Hz ,omega2 = 6.3629Hz, omega3 = 9.2527Hz
2. Rama płaska, model bez lin, podział na węzły i elementy zgodny z geometrią konstrukcji zagęszczony w elementach obciążonych ciągle (rygle), obciążona ciężarem własnym konstrukcji oraz obc. użytkowym.
Ciężar własny i pozostałe obciążenie zastąpiono masami skupionymi przyłożonymi do węzłów elementów poziomych (rygli.) Uwzględniono wpływ sił osiowych na podatność konstrukcji na drgania. Siły przyłożono do węzłów trzonu konstrukcji.
Rys.4. Przyjęty model oraz rozkład mas i sił na kondygnacji.
Otrzymane wyniki

Rys.5. Postacie oraz częstości drgań własnych, omega1 = 2.0247Hz, omega2 = 6.3014Hz, omega3 = 8.9880Hz.
3. Rama płaska, model bez lin, podział na węzły i elementy zgodny z geometrią konstrukcji zagęszczony w elementach obciążonych ciągle (rygle), obciążona ciężarem własnym konstrukcji oraz obc. użytkowym.
Ciężar własny i pozostałe obciążenie zastąpiono masami skupionymi przyłożonymi do węzłów elementów poziomych (rygli.)
Rys.6. Przyjęty model oraz rozkład mas na kondygnacji.
Otrzymane wyniki

Rys.7. Postacie oraz częstości drgań własnych, omega1 = 2.1003Hz, omega2 = 6.4071Hz, omega3 = 9.0396Hz.
4. Rama płaska (bez lin), podział na węzły i elementy zgodny z geometrią konstrukcji, obciążona ciężarem własnym konstrukcji oraz obc. użytkowym.
Obciążenie to przedstawiono sumarycznie jako obciążenie ciągłe i przyłożono je w postaci mas skupionych do węzłów elementów poziomych (rygli). W sumie wartość przyłożonej masy 47000kg co równoważy działające obciążenie. Elementy przyjęto jako nieważkie Ro=0.
Rys.8. Przyjęty model oraz rozkład mas na kondygnacji.
Otrzymane wyniki

Rys.9. Postacie oraz częstości drgań własnych, omega1 = 2.0920Hz omega2 = 5.9232Hz omega3 = 7.0130Hz
5. Rama płaska, model bez lin, podział na węzły i elementy zgodny z geometrią konstrukcji, obciążona ciężarem własnym konstrukcji oraz obc. użytkowym.
Ciężar własny uwzględniono poprzez podanie Ro=7850 kg/m3, pozostałe obciążenie zastąpiono masami skupionymi przyłożonymi do węzłów elementów poziomych (rygli.) Ciężar pojedyńczej kondygnacji wynosi 2700.167kg, pzostała wartość to 44299.84kg, dla ostatniej kondygnacji odpowiednio 2393.523kg i 44606.477kg.
Rys.10. Przyjęty model oraz rozkład mas na kondygnacji.
Otrzymane wyniki

Rys.11. Postacie oraz częstości drgań własnych, omega1 = 2.0951Hz omega2 = 6.0065Hz omega3 = 7.2047Hz
6. Rama płaska (bez lin), model konstrukcji ograniczono do trzonu podział na węzły i elementy zgodny z geometrią konstrukcji, obciążona ciężarem własnym konstrukcji oraz obc. użytkowym.
Obciążenie to przedstawiono sumarycznie jako obciążenie ciągłe i przyłożono je w postaci mas skupionych do węzłów elementów poziomych (rygli). Obciążenie przyłożono do trzonu konstrukcji. Elementy przyjęto jako nieważkie Ro=0.
Rys.12. Przyjęty model oraz rozkład mas na kondygnacji.
Otrzymane wyniki

Rys.13. Postacie oraz częstości drgań własnych, omega1 = 2.3466Hz omega2 = 7.1523Hz omega3 = 11.1952Hz.
7. Rama płaska zamodelowana jako wspornik, podział na elementy zgodny z geometrią konstrukcji, jeden element to jedna kondygnacja, obciążenie sumacyjne przyłożono w postaci mas skupionych w węzłach modelu.
Wartość bezwładności w kierunku osi x Bx=47000kg, w kierunku osi y By=47000, bezwładność obrotowa Jz=0.0. Dane geometryczne, pole przekroju oraz moment bezwładności na zginanie, obliczono dla przekroju złożonego z dwóch elementów słupów (dwie rury czworościenne) rozsuniętych na odległość 4.2m (taką, jaki jest rozstaw słupów).
Rys.14. Przyjęty model oraz przyjęty przekrój elementów.
Otrzymane wyniki

Rys.15. Postacie oraz częstości drgań własnych, omega1 = 2.7354Hz omega2 = 17.187Hz omega3 = 24.748Hz.
Zestawienie przyjętych modeli i otrzymanych wyników.
| Przyjęty model | omega1[Hz] | omega2[Hz] | omega3[Hz] |
|---|---|---|---|
| 1. Rama płaska, model z linami gęsty rozkład mas na elementach poziomych, pręty nieważkie -- całkowite obciążenie zastąpione masami skupionymi, uwzględniony wpływ sił osiowych w elementach. | 2.0336 | 6.3629 | 9.2527 |
| 2. Rama płaska, model bez lin gęsty rozkład mas na elementach poziomych, pręty nieważkie -- całkowite obciążenie zastąpione masami skupionymi, uwzględniony wpływ sił osiowych w elementach. | 2.0247 | 6.3014 | 8.9880 |
| 3. Rama płaska, model bez lin gęsty rozkład mas na elementach poziomych, pręty nieważkie -- całkowite obciążenie zastąpione masami skupionymi, |
2.1003 | 6.4071 | 9.0396 |
| 4. Rama płaska, model bez lin rzadki rozkład mas na elementach poziomych, pręty nieważkie -- całkowite obciążenie zastąpione masami skupionymi, | 2.0920 | 5.9232 | 7.0130 |
| 5. Rama płaska, model bez lin rzadki rozkład mas na elementach poziomych, masa modelu uwzględnina poprzez podanie gęstości i wymiarów elementów, pozostałe obciążenie zastąpione masami skupionymi, | 2.0951 | 6.0065 | 7.2047 |
| 6. Rama płaska, model -- sam trzon budynku pręty nieważkie -- całkowite obciążenie zastąpione masami skupionymi przyłożonymi do dwóch węzłów na każdej kondygnacji, | 2.3466 | 7.1523 | 11.1952 |
| 7. Rama płaska, model -- wspornik pręty nieważkie -- całkowite obciążenie zastąpione masami skupionymi przyłożonymi do węzła na poziomie każdej kondygnacji, | 2.7354 | 17.187 | 24.748 |