
RAMA PŁASKA Z ŁUKIEM
Dla danej ramy płaskiej obliczyć siły przekrojowe, przemieszczenia i reakcje.
łuk został zamodelowany elementami prostoliniowymi. Współrzędne węzłów
na łuku wygenerowano we współrzędnych biegunowych, a następnie dokonano ich zamiany na współrzędne kartezjańskie
-- komenda zuw.
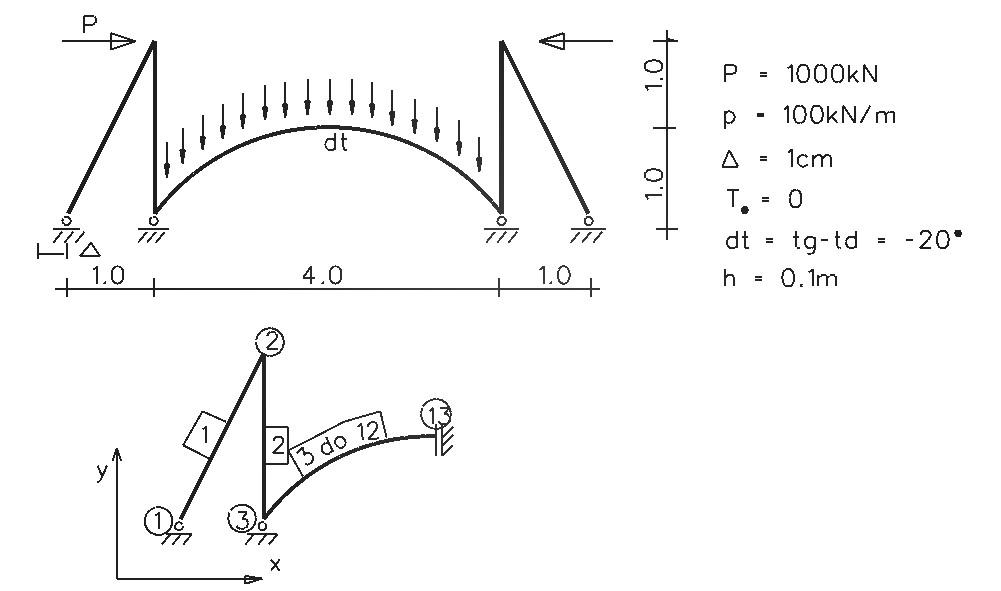
Rys.1. Model ramy z zaznaczonym obciążeniem, warunkami brzegowymi; siatka podziału
na węzły i elementy.
przyjęto: E=21.0*1010N/m2
AlfaT=0.000012
A=0.01m2
Jz=0.0001m4
ROZPOCZĘCIE PRACY
$ feas - wejście do systemu feas
FEAS> - system zgłasza gotowość do pracy
OPIS KONSTRUKCJI
FEAS> ok - wejście do podsystemu OK - Opis Konstrukcji
Podaj rodzaj konstrukcji r2 - r2 - symbol ramy płaskiej,
OK> - podsystem zgłasza gotowość do pracy
wczytanie współrzędnych wezłów
OK> w w-1 0 0 - węzeł o nazwie w-1 ma współrzędne (0,0)
OK> w w-2 1 2 - węzeł o nazwie w-2 ma współrzędne (1,2)
generowanie węzłów na łuku (luk kołowy o promieniu
r=2.5, środku w punkcie (3,1.5)
OK> w w-3 2.5 143.13 - współrzędne węzła w-3
we współrzędnych biegunowych r=2.5 A1=143.13
OK> w w-4 2.5 90 - współrzędne węzła w-4 we współrzędnych
biegunowych r=2.5 A2=90
OK> gw w-3 w-4 9 - wygenerowanie 9 węzłów (we współrzędnych
biegunowych) na odcinku od w-3 do w-4, nadane zostaną im nazwy od w-3 do w-13
OK> zuw w-3 do w-13 3 -1.5 - zamiana współrzędnych węzłów z układu
biegunowego na kartezjański. Współrzędne środka układu biegunowego x=3, y=-1.5
wczytanie danych materiałowych
OK> m m1 - wczytanie danych materiałowych o nazwie mat
MAT: Ro=0 ?> 0
MAT: E=0 ?> 0.21e12 -- wpisujemy wartości odpowiednich stałych,
MAT: AlfaT=0 ?> 0.000012
geometria przekroju
OK> g g1 - wczytanie danych geometrycznych o nazwie g1
GEOM: A=0 ?> 0.01
GEOM:Jz=0 ?>0.1e-4 -- wpisujemy wartości odpowiednich stałych,
elementy
OK> e e-1 w-1 w-2 - element o nazwie e-1 ma węzeł początkowy w-1
końcowy w-2,
OK> e e-2 w-2 w-3 - opis elementu o nazwie e-2
generowanie elementów na łuku
OK> e e-3 w-3 w-4 - opis elementu o nazwie e-3, jest on wzorcowym elementem dla generatora
OK> ge e-3 1 1 10 - wygenerowanie 10 elementów na wzór
elementu e-3, przyrost numeracji elementów 1, przyrost numeracji węzłów 1,
elementom zostaną nadane nazwy od e-3 do e-12
OK> pe e-1 do e-12 m1 g1 - przyporządkowanie elementom od e-1
do e-12 materiału m1 i geometrii g1
warunki brzegowe (w układzie globalnym) z uwzględnieniem obc.
geometrycznego (przesunięcie podpory)
OK> wb w-1 ux uy -0.01 - w węźle w-1 blokujemy dwa przesuwy ux i uy,
uwzględniamy przesuw podpory w kierunku osi x = -0.01m
OK> wb w-3 ux uy - węzeł w-3 nie ma możliwości przesuwu ux i uy
OK> wb w-13 ux fiz - węzeł w-13 nie ma możliwości przesuwu ux i obrotu fiz
siły wezłowe (w układzie globalnym)
OK> sw w-2 1000000 0 0 w węźle w-2 przykładamy siłę skupioną o
wartościach Px=1000000N Py=0 Mz=0
obciążenie elementowe statyczne
OK> uoe g - zakładamy , że całe obciążenie
elementowe podawane będzie w układzie globalnym (komendę wykonuje się raz dla całej konstrukcji)
OK> oe oe-1 łn - wczytanie obiążenia elementowego o nazwie
oe-1, jest to obciążenie liniowo-zmienne na długości
elementu (opcja /ln)
OE:px1=0 ?> 0
OE:py1=0 ?> -100000
OE:mz1=0 ?> 0 - wczytanie wartości danego obciążenia
OE:px2=0 ?> 0
OE:py2=0 ?> -100000
OE:mz2=0 ?> 0
OE:ksi1=0 ?> 0
OE:ksi2=0 ?> 1
OK> pe e-3 do e-12 oe-1 - przyporządkowanie elementom od e-3 do e-12 obciążenia
liniowego o nazwie oe-1
obciążenie elementowe termiczne
OK> oe oe-2 /te - opis obciążenia elementowego
temperaturą
OE:To=0 ?> 0 - wartość przyrostu temperatury
OE:DTy/Hy=0 ?> --200 - iloraz różnicy temperatur
i
wysokości przekroju
Ok> pe e-3 do e-12 oe-2 - przypisanie obciążenia o nazwie oe-2
do elementów od e-3 do e-12
WYJŚCIE Z PODSYSTEMU OK - ROZWIĄZANIE ZADANIA
OK> zap zad3 - zapisanie danych do zadania do pliku ZAD3
TYTUL> Rama plaska - zadanie z lukiem
OK> .. - wyjście z podsystemu OK
FEAS> ro s - rozwiązanie zadania (statyka)
WYŚWIETLENIE WYNIKÓW
FEAS> WS - wejście do podsystemu ws
WS> pm - wyświetlenie przemieszczeń
WS> ne - wyświetlenie sił przekrojowych w elementach
WS> r - wyświetlenie reakcji podporowych
WS> dp - definiowanie pliku wynikowego
podaj nazwe pliku: a - plik wynikowy będzie miał nazwę A.PRN
WS> pm /p - zapisanie przemieszczeń do pliku a, analogicznie
możemy zapisać przemieszczenia, siły przekrojowe (ne), reakcje (r)...
WS> .. - wyjście z podsystemu
GRAFICZNA PREZENTACJA WYNIKÓW
FEAS> GRAF - wejście do podsystemu GRAF
GRAF> si - rysowanie siatki elementów
GRAF> pm - rysowanie przemieszczeń konstrukcji
GRAF> np n - rysuje wykres sił normalnych N
GRAF> np ty - rysuje wykres sił poprzecznych Ty
GRAF> np mz - rysuje wykres momentów Mz
GRAF> o /lg - definiowanie okna na ekranie np. /lg - lewe górne
GRAF> .. - wyjście z podsystemu
ZAKOŃCZENIE PRACY
FEAS> ..
Czy chcesz zakonczyc prace (t/n) t
$
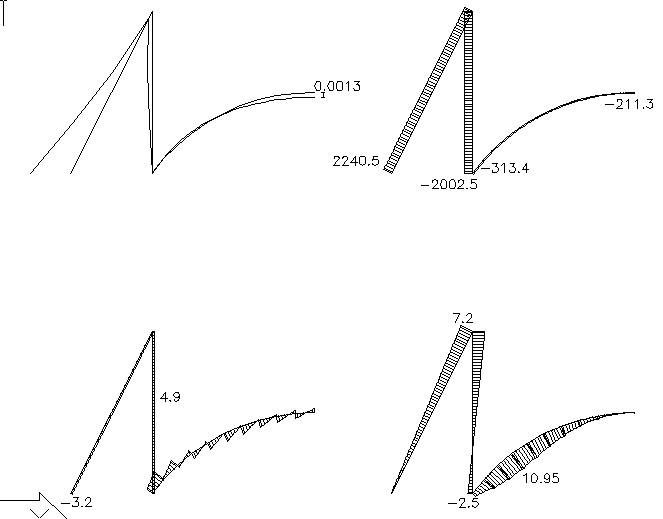
Rys.2. Otrzymane wyniki: wykres przemieszczeń, sił podłużnych, sił poprzecznych i
momentów zginających.
Dla danej ramy płaskiej obliczyć siły przekrojowe, przemieszczenia i reakcje. łuk został zamodelowany elementami prostoliniowymi. Współrzędne węzłów na łuku wygenerowano we współrzędnych biegunowych, a następnie dokonano ich zamiany na współrzędne kartezjańskie -- komenda zuw.

Rys.1. Model ramy z zaznaczonym obciążeniem, warunkami brzegowymi; siatka podziału na węzły i elementy.
przyjęto: E=21.0*1010N/m2
AlfaT=0.000012
A=0.01m2
Jz=0.0001m4
Rys.2. Otrzymane wyniki: wykres przemieszczeń, sił podłużnych, sił poprzecznych i
momentów zginających.
$ feas - wejście do systemu feas
FEAS> - system zgłasza gotowość do pracy
FEAS> ok - wejście do podsystemu OK - Opis Konstrukcji
Podaj rodzaj konstrukcji r2 - r2 - symbol ramy płaskiej,
OK> - podsystem zgłasza gotowość do pracy
OK> w w-1 0 0 - węzeł o nazwie w-1 ma współrzędne (0,0)
OK> w w-2 1 2 - węzeł o nazwie w-2 ma współrzędne (1,2)
OK> w w-3 2.5 143.13 - współrzędne węzła w-3
we współrzędnych biegunowych r=2.5 A1=143.13
OK> w w-4 2.5 90 - współrzędne węzła w-4 we współrzędnych
biegunowych r=2.5 A2=90
OK> gw w-3 w-4 9 - wygenerowanie 9 węzłów (we współrzędnych
biegunowych) na odcinku od w-3 do w-4, nadane zostaną im nazwy od w-3 do w-13
OK> zuw w-3 do w-13 3 -1.5 - zamiana współrzędnych węzłów z układu
biegunowego na kartezjański. Współrzędne środka układu biegunowego x=3, y=-1.5
OK> m m1 - wczytanie danych materiałowych o nazwie mat
MAT: Ro=0 ?> 0
MAT: E=0 ?> 0.21e12 -- wpisujemy wartości odpowiednich stałych,
MAT: AlfaT=0 ?> 0.000012
OK> g g1 - wczytanie danych geometrycznych o nazwie g1
GEOM: A=0 ?> 0.01
GEOM:Jz=0 ?>0.1e-4 -- wpisujemy wartości odpowiednich stałych,
OK> e e-1 w-1 w-2 - element o nazwie e-1 ma węzeł początkowy w-1
końcowy w-2,
OK> e e-2 w-2 w-3 - opis elementu o nazwie e-2
OK> e e-3 w-3 w-4 - opis elementu o nazwie e-3, jest on wzorcowym elementem dla generatora
OK> ge e-3 1 1 10 - wygenerowanie 10 elementów na wzór
elementu e-3, przyrost numeracji elementów 1, przyrost numeracji węzłów 1,
elementom zostaną nadane nazwy od e-3 do e-12
OK> pe e-1 do e-12 m1 g1 - przyporządkowanie elementom od e-1
do e-12 materiału m1 i geometrii g1
OK> wb w-1 ux uy -0.01 - w węźle w-1 blokujemy dwa przesuwy ux i uy,
uwzględniamy przesuw podpory w kierunku osi x = -0.01m
OK> wb w-3 ux uy - węzeł w-3 nie ma możliwości przesuwu ux i uy
OK> wb w-13 ux fiz - węzeł w-13 nie ma możliwości przesuwu ux i obrotu fiz
OK> sw w-2 1000000 0 0 w węźle w-2 przykładamy siłę skupioną o
wartościach Px=1000000N Py=0 Mz=0
OK> uoe g - zakładamy , że całe obciążenie
elementowe podawane będzie w układzie globalnym (komendę wykonuje się raz dla całej konstrukcji)
OK> oe oe-1 łn - wczytanie obiążenia elementowego o nazwie
oe-1, jest to obciążenie liniowo-zmienne na długości
elementu (opcja /ln)
OE:px1=0 ?> 0
OE:py1=0 ?> -100000
OE:mz1=0 ?> 0 - wczytanie wartości danego obciążenia
OE:px2=0 ?> 0
OE:py2=0 ?> -100000
OE:mz2=0 ?> 0
OE:ksi1=0 ?> 0
OE:ksi2=0 ?> 1
OK> pe e-3 do e-12 oe-1 - przyporządkowanie elementom od e-3 do e-12 obciążenia
liniowego o nazwie oe-1
OK> oe oe-2 /te - opis obciążenia elementowego
temperaturą
OE:To=0 ?> 0 - wartość przyrostu temperatury
OE:DTy/Hy=0 ?> --200 - iloraz różnicy temperatur
i
wysokości przekroju
Ok> pe e-3 do e-12 oe-2 - przypisanie obciążenia o nazwie oe-2
do elementów od e-3 do e-12
OK> zap zad3 - zapisanie danych do zadania do pliku ZAD3
TYTUL> Rama plaska - zadanie z lukiem
OK> .. - wyjście z podsystemu OK
FEAS> ro s - rozwiązanie zadania (statyka)
FEAS> WS - wejście do podsystemu ws
WS> pm - wyświetlenie przemieszczeń
WS> ne - wyświetlenie sił przekrojowych w elementach
WS> r - wyświetlenie reakcji podporowych
WS> dp - definiowanie pliku wynikowego
podaj nazwe pliku: a - plik wynikowy będzie miał nazwę A.PRN
WS> pm /p - zapisanie przemieszczeń do pliku a, analogicznie
możemy zapisać przemieszczenia, siły przekrojowe (ne), reakcje (r)...
WS> .. - wyjście z podsystemu
FEAS> GRAF - wejście do podsystemu GRAF
GRAF> si - rysowanie siatki elementów
GRAF> pm - rysowanie przemieszczeń konstrukcji
GRAF> np n - rysuje wykres sił normalnych N
GRAF> np ty - rysuje wykres sił poprzecznych Ty
GRAF> np mz - rysuje wykres momentów Mz
GRAF> o /lg - definiowanie okna na ekranie np. /lg - lewe górne
GRAF> .. - wyjście z podsystemu
FEAS> ..
Czy chcesz zakonczyc prace (t/n) t
$
