|
Dla danej płyty balkonowej o wymiarach 3x1.6m. obliczyć przemieszczenia i
siły przekrojowe od obciążenia ciągłego. Balkon zamodelowano rusztem
wspornikowym.
Jako obciążenie przyjęto sumę ciężaru płyty żelbetowej o grubości
0.12 m (0.12*25000*1.1= 3300 N/m2), oraz obciążenie normowe balkonu
(5000*1.3=6500 N/m2) co daje łącznie 9800 N/m2. Obciążenie to rozłożono
na poszczególne elementy.Na elementy e-1, e-4 działa obciążenie
Q1= 3369 N/m , na elementy e-12, e-13, e-14 obciążenie Q2= 4820 N/m , na elementy e-9, e-10, e-11
obciążenie Q3= 2352 N/m , na elementy e-2, e-3 obciążenie Q4= 6738 N/m ,
na elementy e-6, e-7 obciążenie Q5= 3920 N/m , na elementy e-5, e-8 obciążenie Q6= 1960 N/m .
Przyjęto E=2.7*1010 N/m2, G=2.025*1010 N/m2.
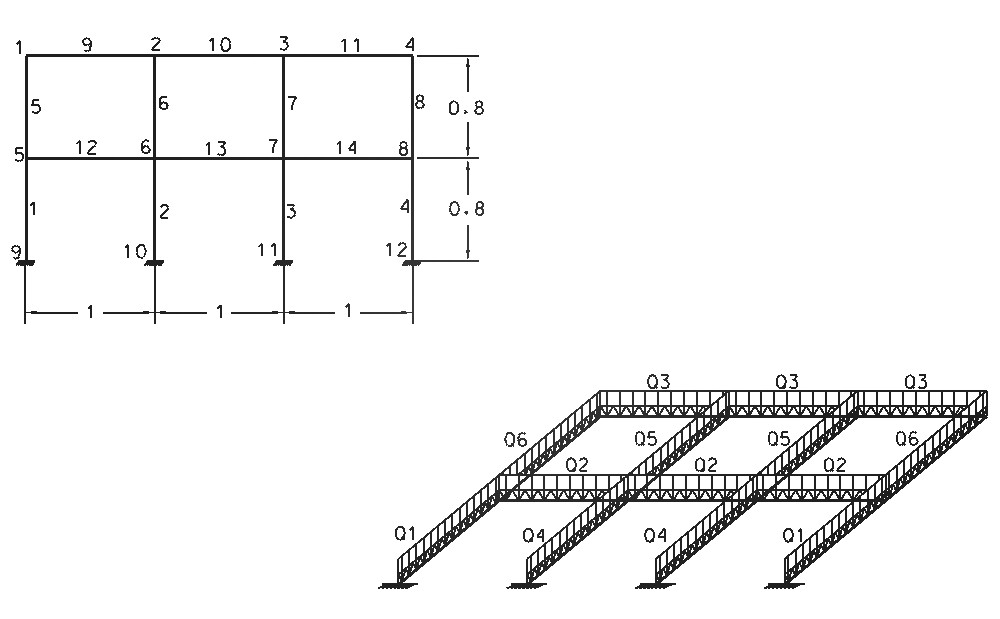
Rys.1. Schemat zadania z zaznaczonym podziałem na węzły i elementy.
ROZPOCZĘCIE PRACY
| feas | - wejście do systemu feas |
| FEAS> | - system zgłasza gotowość do pracy |
OPIS KONSTRUKCJI
| FEAS> ok | - wejście do podsystemu OK - Opis Konstrukcji |
| Podaj rodzaj konstrukcji ru | - ru - symbol rusztu | ,
| OK> | - podsystem zgłasza gotowość do pracy |
wprowadzenie stałych materialowych konstrukcji
| OK> m mat | - stałe zapamiętane pod nazwą mat |
| MAT:Ro=0 ?>0 | - gęstość materiału |
| MAT:E=0 ?>2.7e10 | - moduł Younga |
| MAT:G=0 ?>2.025e10 | - moduł Kirchhoffa |
| MAT:Alft=0 ?>0 | - współczynnik rozszerzalności cieplnej |
wprowadzenie charakterystyk geometrycznych
| OK> g
| | NazGeom ? geo1
| - charakterystyki zapamiętane pod nazwą geo |
| GEOM:A=0 ?>0.084 | - pole powierzchni przekroju |
| GEOM:Js=0 ?>0.000359 | - charakterystyka przekroju na skręcanie |
| GEOM:Jy=0 ?>0.0001008 | - moment bezwładności Jy |
| GEOM:Jz=0 ?>0.00343 | - moment bezwładności Jz |
| OK> g geo2
| | GEOM:A=0 ?>0.042
| | GEOM:Js=0 ?>0.0001572
| | GEOM:Jy=0 ?>0.0000504
| | GEOM:Jz=0 ?>0.0004288
| | OK> g geo3
| | GEOM:A=0 ?>0.096
| | GEOM:Js=0 ?>0.0004167
| | GEOM:Jy=0 ?>0.000115
| | GEOM:Jz=0 ?>0.00512
| | OK> g geo4
| | GEOM:A=0 ?>0.048
| | GEOM:Js=0 ?>0.0001859
| | GEOM:Jy=0 ?>0.0000576
| | GEOM:Jz=0 ?>0.00064
|
wprowadzenie współrzednych węzłow
| OK> W | - wejście w tryb wprowadzania węzłów |
| W:X=?,Y=?>w-1 0 1.6 /y | - wprowadzenie wsp. punktu w-1
parametr /y oznacza ,że dalsze węzły
mają taką samą wsp. y |
| W:X=?,Y=1.6> w-2 1 | - podajemy tylko x |
| W:X=?,Y=1.6> w-3 2
| | W:X=?,Y=1.6> w-4 3 /y | - likwidacja opcji /y |
| W:X=?,Y=?>w-5 0 0.8 /y | - ustalenie nowego y |
| W:X=?,Y=0.8> w-6 1 | - podajemy tylko x |
| W:X=?,Y=0.8> w-7 2
| | W:X=?,Y=0.8> w-8 3 /y | - likwidacja opcji /y |
| W:X=?,Y=?>w-9 0 0 /y | - ustalenie nowego y |
| W:X=?,Y=0> w-10 1 | - podajemy tylko x |
| W:X=?,Y=0> w-11 2
| | W:X=?,Y=0> w-12 3 /y | - likwidacja opcji /y |
| W:X=?,Y=0> .. | - wyjście z trybu wprowadzania węzłow |
wprowadzenie elementow
| OK> e e-1 w-9 w-5 | - wprowadzenie elementu e-1 o węzłach
początkowym i końcowym w-9,w-5 |
| OK> ge e-1 1 1 4 | - wygenerowanie 4 elementów na wzór elementu
e-1, przyrost numeracji pierwszego węzła elementu1, drugiego1 |
| OK> e e-5 w-5 w-1
| | OK> ge e-5 1 1 4
| | OK> e e-9 w-1 w-2
| | OK> ge e-9 1 1 3
|
| OK> e e-12 w-5 w-6
| | OK> ge e-12 1 1 3
|
przyporządkowanie danych materiałowych i geometrycznych
do elementów
| OK> pe e-2 e-3 e-6 e-7 mat geo1
| | OK> pe e-1 e-4 e-5 e-8 mat geo2
| | OK> pe e-12 do e-14 mat geo3
| | OK> pe e-9 do e-11 mat geo4
|
definiowanie warunków brzegowych.
| OK> wb w-9 do w-12 uz fix fiy | - zamocowanie w węzłach od w-9 do w-12 |
wprowadzenie obciążeń elementowych.
| OK> oe
| | NazOE ?q1 | - nazwa obciążenia |
| Opcja ?/ln | - opcja oznacza obciążenie ciągłe |
| OE:pz1=0 ?> -3369 | - wartość początkowa składowej z |
| OE:mx1=0 ?> | - wartość początkowa ciągłych momentów mx |
| OE:my1=0 ?> | - wartość początkowa ciągłych momentów my |
| OE:pz2=0 ?> -3369 | - wartość końcowa składowej z |
| OE:mx2=0 ?> | - wartość końcowa ciągłych momentów mx |
| OE:my2=0 ?> | - wartość końcowa ciągłych momentów mx |
| OE:ksi1=0 ?> | - początek oddziaływania obciążenia we współrzędnych bezwymiarowych |
| OE:ksi2=0 ?> 1 | - koniec oddziaływania obciążenia |
| OK> oe q2 /ln | - wprowadzenie obciążenia o nazwie q2 |
| OE:pz1=0 ?> -4820
| | OE:mx1=0 ?>
| | OE:my1=0 ?>
| | OE:pz2=0 ?> -4820
| | OE:mx2=0 ?>
| | OE:my2=0 ?>
| | OE:ksi1=0 ?>
| | OE:ksi2=0 ?> 1
| | OK> oe q3 /ln
| | OE:pz1=0 ?> -2352
| | OE:mx1=0 ?>
| | OE:my1=0 ?>
| | OE:pz2=0 ?> -2352
| | OE:mx2=0 ?>
| | OE:my2=0 ?>
| | OE:ksi1=0 ?>
| | OE:ksi2=0 ?> 1
| | OK> oe q4 /ln
| | OE:pz1=0 ?> -6738
| | OE:mx1=0 ?>
| | OE:my1=0 ?>
| | OE:pz2=0 ?> -6738
| | OE:mx2=0 ?>
| | OE:my2=0 ?>
| | OE:ksi1=0 ?>
| | OE:ksi2=0 ?> 1
|
| OK> oe q5 /ln
| | OE:pz1=0 ?> -3920
| | OE:mx1=0 ?>
| | OE:my1=0 ?>
| | OE:pz2=0 ?> -3920
| | OE:mx2=0 ?>
| | OE:my2=0 ?>
| | OE:ksi1=0 ?>
| | OE:ksi2=0 ?> 1
| | OK> oe q6 /ln
| | OE:pz1=0 ?> -1960
| | OE:mx1=0 ?>
| | OE:my1=0 ?>
| | OE:pz2=0 ?> -1960
| | OE:mx2=0 ?>
| | OE:my2=0 ?>
| | OE:ksi1=0 ?>
| | OE:ksi2=0 ?> 1
|
przypisanie wprowadzonych obciążeń odpowiednim elementom
| OK> pe e-1 e-4 q1
| | OK> pe e-12 do e-14 q2
| | OK> pe e-9 do e-11 q3
| | OK> pe e-2 e-3 q4
| | OK> pe e-6 e-7 q5
| | OK> pe e-5 e-8 q6
|
zapis wprowadzonych danych do zbioru o nazwie ruszt
| OK> zap ruszt
| | TYTUL> Balkon modelowany rusztem.
|
WYJŚCIE Z PODSYSTEMU OK I ROZWIĄZANIE ZADANIA
GRAFICZNA PREZENTACJA WYNIKÓW
| FEAS> graf | - przejście do podsystemu graficzej prezentacji wyników |
| GRAF> izom | - widok aksonometryczny |
| GRAF> si | - schemat rusztu |
| GRAF> wb | - schemat podpór |
| GRAF> np tz 5 /c | - narysowanie wykresu siły poprzecznej,
5 wspólczynnik skali (można pominąc),
/c - opcja powodująca zakreskowanie wykresu |
| GRAF> ce | - wyczyszczenie ekranu |
| GRAF> si | - schemat rusztu |
| GRAF> np my /c | - rysowanie wykresu momentu zginającego my |
| GRAF> ce | - wyczyszczenie ekranu |
| GRAF> si | - schemat rusztu |
| GRAF> np ms /c | - rysowanie wykresu momentu skręcającego |
| GRAF> ce | - wyczyszczenie ekranu |
| GRAF> pm | - wyświetlenie postaci odkształconej |
| GRAF> .. | - wyjście z podsystemu GRAF |
WYŚWIETLENIE WYNIKÓW
| FEAS> ws | - wejście do podsystemu wyświetlania wyników |
| WS> r | - wyświetlenie reakcji podporowych |
| WS> pm | - wyświetlenie przemieszczeń w węzłach |
| WS> ne | - wyświetlenie wartości sił przekrojowych w węzłach |
| WS> .. | - wyjście z WS |
ZAKOŃCZENIE PRACY
| FEAS> .. | - wyjście z FEAS`a.
|
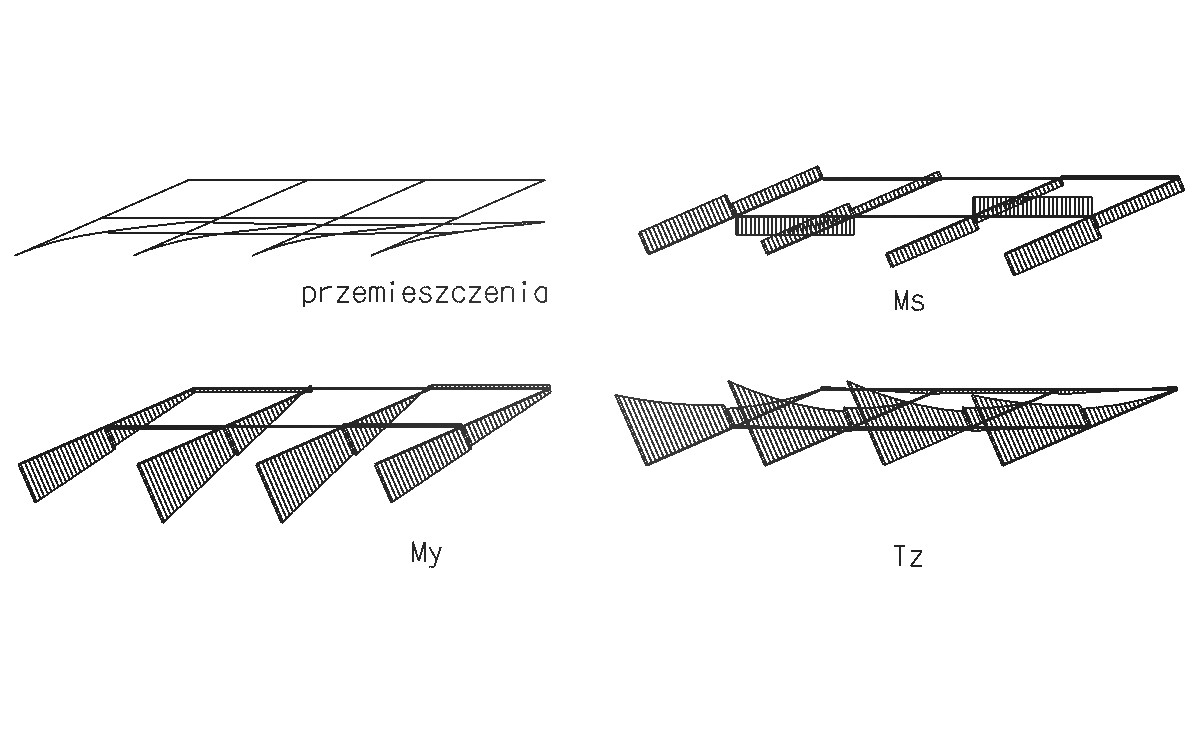
Rys.2. Otrzymane wyniki, odpowiednio wykres przemieszczeń, momentów
skręcających, momentów zginających i siły poprzecznej.
|


