|
Realizowane sferyczne kopu�y pr�towe s� konstrukcjami z�o�onymi z pr�t�w
po��czonych w w�z�ach le��cych na powierzchni kuli.
Opr�cz warunk�w, kt�re musi spe�nia� ta konstrukcja ze wzgl�du na
mechanik�,
wymaga si� aby elementy przekrycia mia�y jednakowe wymiary lub �eby liczba
r�nych typ�w element�w by�a jak najmniejsza.
W praktyce
najcz�ciej realizowanych jest 5 rodzaj�w tego typu przekry�. W pracy tej
opracowano algorytmy i oprogramowano generatory nast�puj�cych podstawowych
struktur:

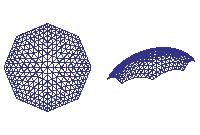
siatka Schwedlera -- sk�ada si� element�w po�o�onych wzd�u�
po�udnik�w
i r�wnole�nik�w sfery. W celu usztywnienia konstrukcji, ka�dy trapez
utworzony
z przeci�cia element�w po�udnik�w i r�wnole�nik�w ma dodatkowo elementy
na przek�tnej. Mo�liwe s� trzy rodzaje skratowania trapez�w: prawosko�nie,
na przemian prawo i lewo sko�nie w kolejnych warstwach, po dwa skratowania
prawo i lewo sko�ne w ka�dym
trapezie.
Ze wzgl�du na znaczne zag�szczenie element�w konstrukcji przy wierzcho�ku
sfery, zdecydowano si� na pozostawienie otworu w generowanej siatce, poprzez
wprowadzenie jako zmiennej k�ta fi2. Domkn�� sfer� mo�na w dowolny spos�b
korzystaj�c z narz�dzi systemu FEAS, lub innego systemu do kt�rego generatory
struktur b�d� do��czone.
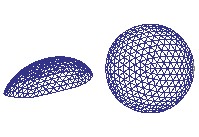
siatka Lamella -- sk�adu si� kilku lub kilkunastu segment�w
zawieraj�cych takie same rodzje element�w. Jest to siatka przewidziana jako
domkni�ta (nie podajemy k�ta fi2). Mo�liwe s� dwie postacie tej siatki,
pierwsza oznaczona liczb� 5 jest siatk� kt�rej rzut poziomy jest wielobokiem,
druga oznaczona liczb� 6 ma rzut poziomy w formie ko�a, a pr�ty obwodowe
znajduj� si� na r�wnole�nikach sfery.
siatka geodezyjna -- siatka zbudowana na podstawie dwudziesto�cianu
foremnego wpisanego w sfer�. Przy poszukiwaniu siatki element�w dla
powierzchni sferycznych d��ymy do tego, aby otrzyma� jak najwi�ksz�
liczb� element�w o jednakowej d�ugo�ci. Warunki takie spe�niaj�
wielo�ciany
foremne. Jako pierwszy etap podzia�u sfery wprowadzono wi�c dwudziesto�cian
foremny ( wszystkie boki r�wne, dalsze zag�szczanie siatki uzyskano poprzez
podzia� �cian dwudziesto�cianu. W literaturze istnieje szereg sposob�w
podzia�u tych �cian w celu ujednolicenia wymiar�w element�w, w naszej
pracy wykonano najprostszy z nich r�wnomierny podzia�.

siatka tr�jk�t�w r�wnoramiennych w ka�dej z warstw -- siatka o
jednakowej liczbie element�w w ka�dej z warstw podzia�u sfery, utworzone z
element�w tr�jk�ty zbiegaj� do tr�jk�t�w r�wnobocznych ( nie zawsze tak
jest ze wzgl�du na zestaw danych pocz�tkowych). Elementy tej siatki silnie
zag�szczaj� si� przy zbli�aniu do wierzcho�ka sfery, dlatego jako parametr
tworzenia siatki ustalono takze k�t pomi�dzy osi� poziom� a g�rnym,
koniecznym otworem. W celu domkni�cia tej siatki przy wierzcho�ku proponujemy
wprowadzenie warstw przej�ciowych zmniejszaj�cych liczb� element�w na
obwodzie o po�ow�, lub domkni�cie przez wprowadzenie element�w promienistych
wychodz�cych z wierzcho�ka sfery.
|




